2.4. Подстановки Эйлера

Предварительно изучите по учебнику Г. М. Фихтен-гольиа главу X, п° 170.

В задачах 228—233 вычислить интегралы от биномиальных дифференциалов, предварительно определив, к какому случаю каждый из них относится.

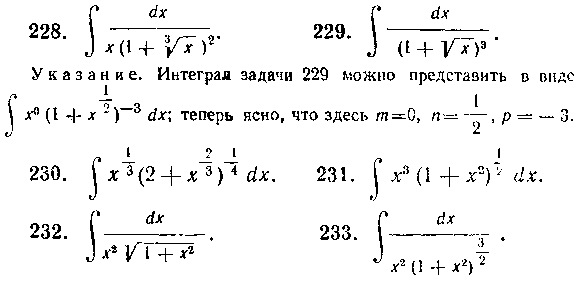
Очень важный класс интегралов:

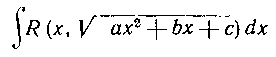
приводится к интегралам от рациональных функций с помощью следующих трех подстановок Эйлера.

I. Если а> 0, то берется подстановка

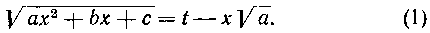
II. Если с> О, то берется подстановка

III. Если квадратный трехчлен имеет различные вещественные корни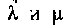, т. е. если

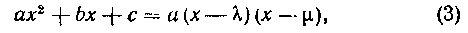
то берется подстановка

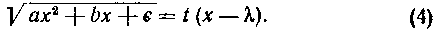
Подстановки Эйлера часто приводят к весьма громоздким выкладкам, поэтому их следует применять лишь тогда, ксгда трудно подыскать другой способ для вычисления заданного интеграла.

234. Найти интеграл:

Решение. Здесь а— I, с=2; следовательно, с одинаковым успехом можно применить как первую, так и вторую подстановки Эйлера. Применим первую подстановку Эйлера:

Возводим в квадрат, делаем приведение подобных:

Подставив в данный интеграл, получим:

Мы получили в результате интеграл от рациональной дроби (случай 2), знаменатель которсй содержит множители первой степени, один из которых повторяется дважды. Пишем разложение на простейшие дроби:

»

Итак, имеем:

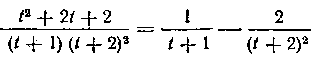
следовательно,

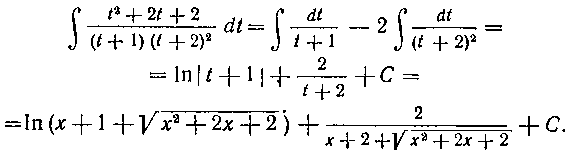
235. Найти интеграл:

Решение. Здесь '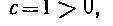~ поэтому применим вторую подстановку Эйлера:

Откуда

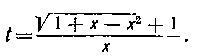
Далее возводим в квадрат, делаем приведение подобных и сокращаем на х:

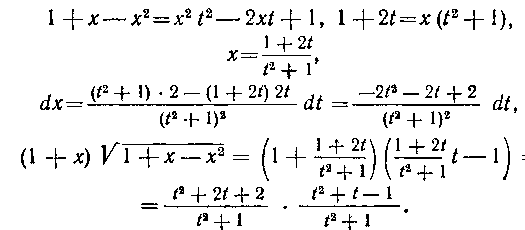
Таким образом,

68

Замечание. Интеграл в задаче 235 берется гораздо проще подстановкой

Убедитесь в этом сами.

236. Найти интеграл:

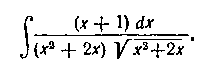
Решение. Квадратный трехчлен имеет. здесь два оазличных вещественных корня:Так как

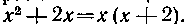Поэтому применяем третью подстановку Эйлера:

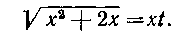
После возведения в квадрат и сокращения на х, получим:

Далее находим:

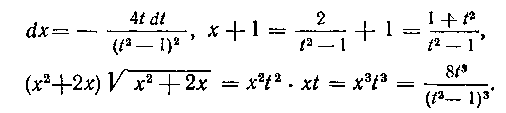
Таким образом, имеем:

В задачах 237—240 вычислите интегралы с помощью одной из подстановок Эйлера.

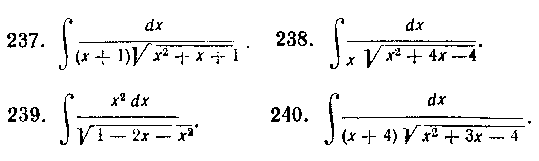
< Предыдущая		Следующая >