2.3. Интегрирование биномиальных дифференциалов

Предварительно изучите по учебнику Г. М. Фихтен-гольца главу X, п° 169.

Биномиальным дифференциалом называется выражение

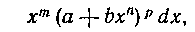
в котором т, п, р — рациональные числа, а, Ь — постоянные, отличные от нуля. Интеграл

берется лишь в следующих трех случаях.

Случай I. Показатель р есть целое число; интегралы берутся аналогично рассмотренным в предыдущем параграфе.

Случай 2.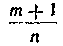Есть целое число; интегралы

берутся подстановкой

Случай 3.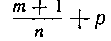Есть целое число; интегралы

берутся подстановкой

Рассмотрим задачи на каждый из указанных случаев.

225. Найти интеграл:

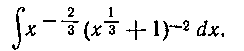
Решение. ЗдесьТ. е.

р—целое число. Интеграл относится к первому случаю; он берется так же, как интегралы, рассмотренные в предыдущем параграфе. Вводим подстановку

Теперь сразу видно, что - и

есть целое число, т. е. мы имеем второй случай, следовательно, здесь нужно ввести подстановку

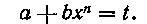
Таким образом, для заданного интеграла берем подстановку

Заданный интеграл равен:

226. Найти интеграл:

Решение. Перепишем наш интеграл в виде

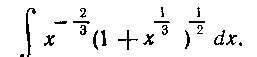
откуда находим

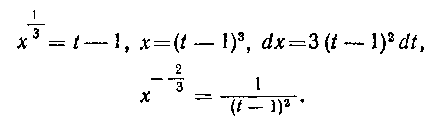
Подставив в интеграл, получим:

227. Найти интеграл:

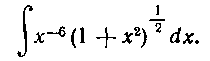
Решение. Здесь. Легко ви

деть, что

есть целое число, т. е. мы имеем третий случай, при котором надо воспользоваться подстановкой ах~-п + 6 = t.

Таким образом, применительно к заданному интегралу мы берем подстановку

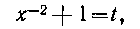
откуда получаем

Итак.

< Предыдущая		Следующая >