2.2. Интегрирование некоторых выражений, содержащих радикалы

Предварительно изучите по учебнику Г. М. Фихтен-гольца главу X, п° 168.

208. Найти интеграл:

Решение. Воспользуемся подстановкой

Имеем:

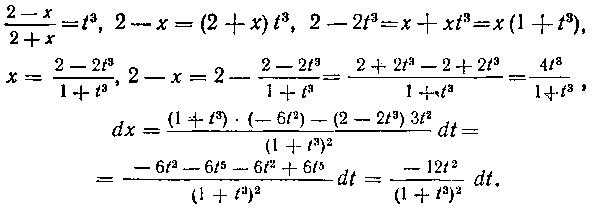
Подставив все полученное в заданный интеграл, будем иметь:

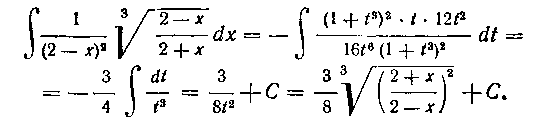
209. Найти интеграл:

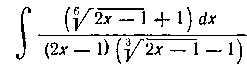
Решение. Введем подстановку 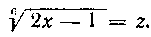Предварительно подготовим все для нашего интеграла:

Подставляя в заданный интеграл, получим:

210. Найти интеграл:

Решение. Преобразуем сначала подынтегральную функцию

а теперь введем подстановку

*) Мы в числителе прибавили z и вычли z.

и интеграл примет вид:

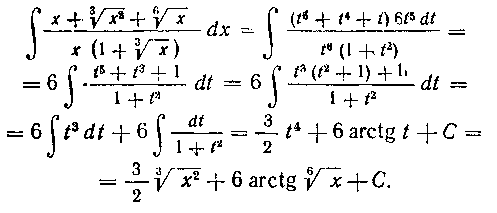
В задачах 212—224, воспользовавшись соответствующими подстановками, вычислить заданные интегралы.

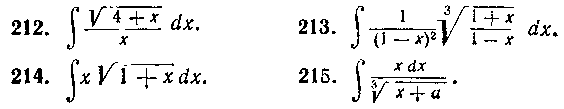
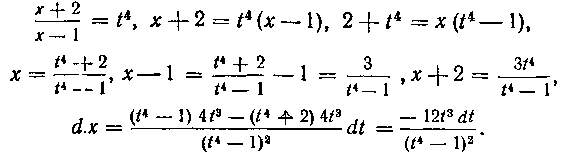
Таким образом, заданный интеграл примет вид:

211. Найти интеграл:

Решение. Чтобы освободиться от всех радикалов, достаточно воспользоваться подстановкой

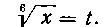
Тогда

Указание. В задаче 216 вынести за знак корня I) (дг—I) (см. решение задачи 210).

< Предыдущая		Следующая >