1.5 Интегралы вида

Интегралы вида

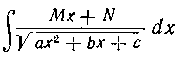
одним из способов приведения квадратного трехчлена к каноническому виду сводятся либо к формуле 10 из таблицы I (при а<0), либо к формуле 11 (при а> 0).

В интегралах более общего вида

мы выделяем сначала в числителе часть, кратную производной трехчлена, и в результате получаем интеграл вида (I).

145. Найти интеграл:

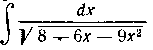
Решение. Числитель подынтегральной функции отличается от производной трехчлена постоянным множителем 4, Поэтому интеграл берется сразу подстановкой

Решение. Приводим квадратный трехчлен к каноническому виду способом добавления до полного квадрата:

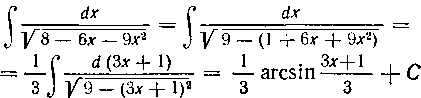
(см. формулу 10 из табл. I). 146. Найти интеграл:

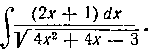
147. Найти интеграл: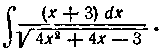

Решение. Сначала выделяем в числителе часть, кратную производной квадратного трехчлена. Так как

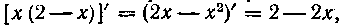
Решение. Выделим в числителе часть, кратную производной от квадратного трехчлена. Получим:

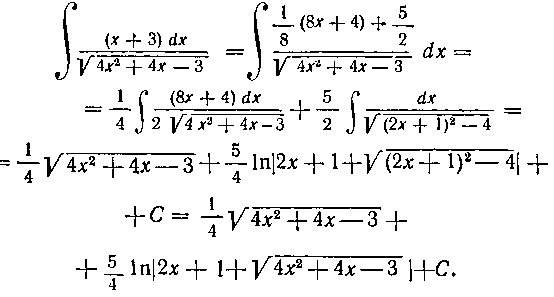
Первый интеграл мы взяли, как в решении задачи 146; второй интеграл подстановкой 2х - J - I —t сразу приводится к формуле 11 из таблицы I.

148. Найти интеграл:

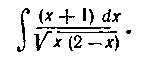
то получим:

К

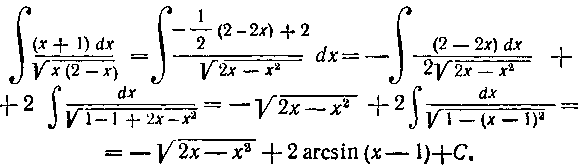
I (рх + q)Vах2 - J - Ьх + с приводятся к интегралам вида (2) подстановкой

Интегралы вида

(Mx + N) dx

Как это делается, показано в решении задачи 60 для случая, когда р = I, q = 0.

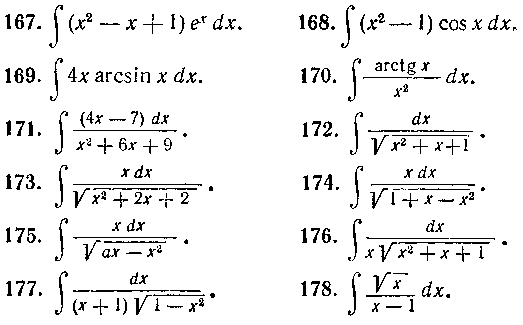
ОСНОВНЫЕ КЛАССЫ ИНТЕГРИРУЕМЫХ ФУНКЦИЙ

< Предыдущая		Следующая >