1.4. Интегралы вида
В интегралы указанного вида входит выражение

которое называют квадратным трехчленом. Выражение
d = Ъ% — 4 ас называют дискриминантом квадратного трехчлена.
Напомним, что если X1 и х2 — корни квадратного трехчлена (I), то
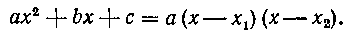
Из элементарной алгебры известно также, что квадратный трехчлен (I)
1) имеет вещественные различные корни, если Ь2 — 4 ас > О,
2) имеет вещественные равные корни, если b2—4 ас—Ot
3) » комплексные сопряженные корни, если £>2 — 4 ас < 0.
Всякий квадратный трехчлен, у которого коэффициент при х в первой степени равен нулю, называется каноническим. Он имеет вид ах2-\-с.
Покажем на примерах, как квадратный трехчлен приводится к каноническому виду.
Первый способ. Пусть дан трехчлен хг-(-х-J - I. Дополняем его до полного квадрата. Чтобы избежать дробных слагаемых, поступаем так:

Такой способ приведения к каноническому виду называется дополнением до полного квадрата. Заметив, что значение г равно производной от квадратного трехчлена по х, мы теперь можем предложить другой способ приведения к каноническому виду.
Второй способ. Привести к каноническому виду трехчлен 5л:2—х -\-2. Производную от трехчлена принимаем за новую переменную:

откуда находим
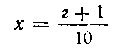
и подставляем это значение х в данный трехчлен: 32

Приведем этот же трехчлен к каноническому виду 1-м способом:
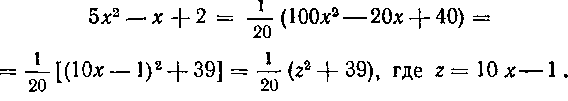
Рассмотрим второй способ в общем виде. За новую переменную z принимаем производную от квадратного трехчлена (I):
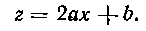
Из полученного равенства находим х как функцию от г\

и подставляем это значение х в трехчлен (I). Мы получим:
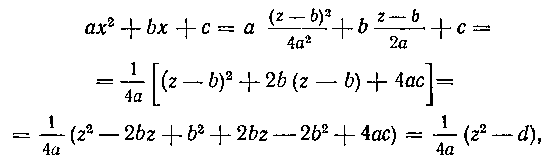
где Есть дискриминант квадратного трех
Есть дискриминант квадратного трех
члена.
Двумя способами привести к каноническому виду трехчлен
I) Имеем:
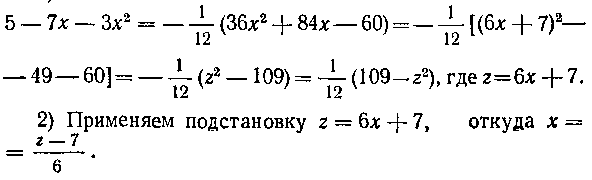
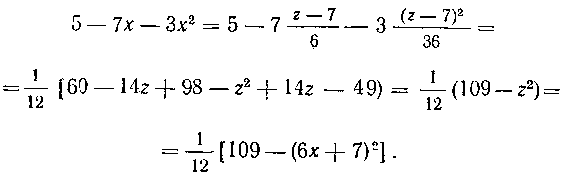
Рассмотрим теперь интегралы вида
Начнем с более простых задач.
127. Найти интеграл:
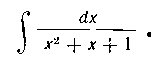
Решение. Применяя подстановку ( , от
( , от
куда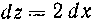 И, следовательно,
И, следовательно, Приведем
Приведем
квадратный трехчлен к каноническому виду (см. стр. 32):

128. Найги интеграл:
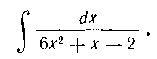
Решение. Применяем подстановку
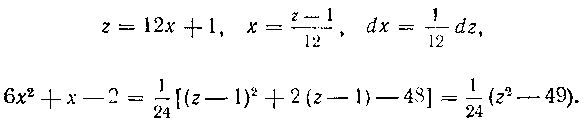

где
Решение. Здесь числитель отличается от производной знаменателя, равной 2х—I, постоянным множителем 5, поэтому

130. Найти интеграл:
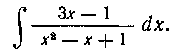
Решение. Здесь числитель не равен производной знаменателя и не отличается от нее постоянным множителем. В таких случаях интеграл можно взять двумя способами.
Первый способ. Аналогично решениям задач 127,
128, применяем подстановку

129. Найти интеграл:
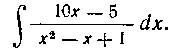
откуда


где
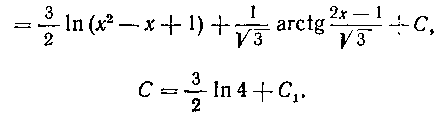
Второй способ. Выделим в числителе часть, кратную производной знаменателя:
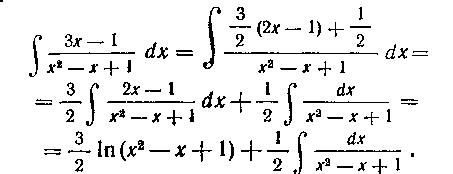
Мы получили более простой интеграл, который возьмем подстановкой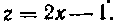 Имеем:
Имеем:

Итак, окончательно

Второй способ решения особенно выгодно применять в случае, когда квадратный трехчлен имеет комплексные корни.
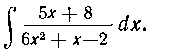
Решение. В данном случае корни квадратного трехчлена вещественны и равны соответственно
 -, следовательно,
-, следовательно,
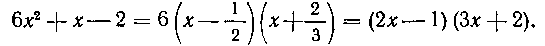
Применим к решению этой задачи способ неопределенных коэффициентов (см. учебник, п° 166). Имеем тождественное равенство:

Приводя к общему знаменателю, приравниваем числители:
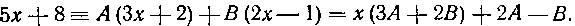
Теперь воспользуемся тем, что в обеих частях тождества коэффициенты при одинаковых степенях х должны быть равны:

Следовательно,
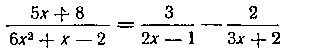
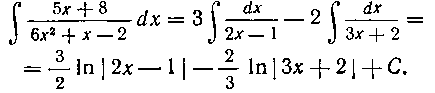
131. Найти интеграл:
132. Найти интеграл:
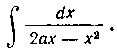
Решение. Знаменатель легко разложить на вещественные множители; применяем способ неопределенных коэффициентов:

Неопределенные коэффициенты А и В можно найти и с помощью такого рассуждения. Тождество (2) справедливо при любом значении х; подставим поэтому в тождество такие значения х, при которых одно из выражений при А или В обращалось бы в нуль. Такими значениями х будут х = 0, х — 2а. Имеем:
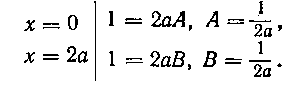
Таким образом,
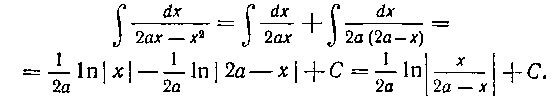
133. Найти интеграл:
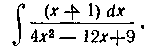
Решение. Здесь квадратный трехчлен имеет два равных вещественных корня, так как Ax2—12х - J - 9 = = (2х — З)2. Выделяем поэтому в числителе часть, кратную 2х—3, разбиваем на два интеграла, которые легко берутся подстановкой 2х — 3 = t:
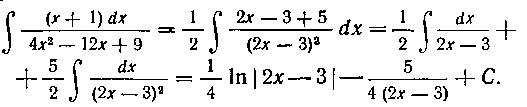
В задачах 134—144 либо приведите квадратный трехчлен к каноническому виду (в случае комплексных корней), либо воспользуйтесь способом неопределенных коэффициентов (в случае вещественных корней).

Указание. В задаче 140 предварительно исключите целую часть.
| < Предыдущая | Следующая > |
|---|