1.3. Способ интегрирования по частям

Предварительно изучите по учебнику Г. М. Фихтен-гольца главу X, п° 162, 163.

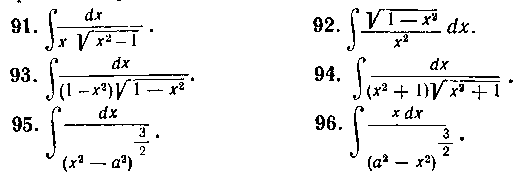
В задачах 91—96 найти интегралы с помощью одной из тригонометрических подстановок.

Интегрированием по частям называется сведение

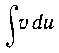заданного интегралаК интегралуС помощью

формулы

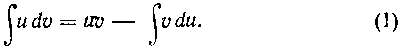
Применяя способ интегрирования по частям, мы должны предварительно представить подынтегральное выражение в виде произведения одной функции на дифференциал другой функции. Дадим два практических совета*

Если подынтегральное выражение представляет собой произведение либо тригонометрической функции на алгебраическую, либо показательной на алгебраическую, то за и следует принимать алгебраическую функцию.

Если в подынтегральное выражение входит множителем либо одна из обратных тригонометрических функций arcsin я, arctg* и др., либо функция In х, то за и следует выбирать одну из указанных функций.

97. Найти интеграл:

Решение. Сначала вводим множитель е~2х под знак дифференциала

Теперь подготовим все необходимое, расположив запись, как показано:

Таким образом, по формуле (I) имеем:

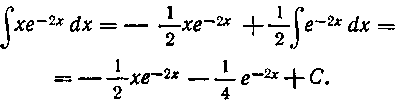
98. Найти интеграл:

Решение. Имеем:

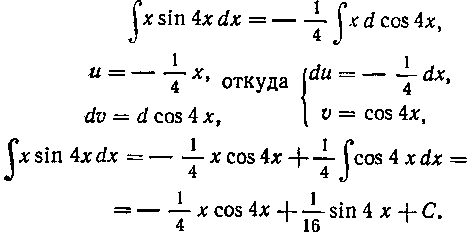
99. Найти интеграл: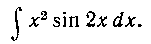 Решение. Имеем:

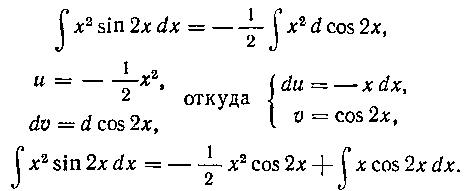
Полученный интеграл еще раз интегрируем по частям:

Итак, окончательно имеем:

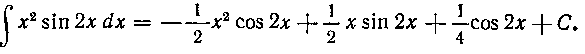
100. Найти интеграл:

Решение. Сначала подводим множитель х под знак дифференциала, затем применяем подстановку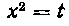 и только после этого интегрируем по частям:

101. Найти интеграл: Решение. Имеем:

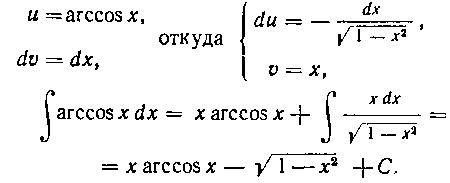
берется подстановкой

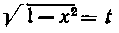
Интеграл

{см. решение задачи 59). 102. Найти интеграл: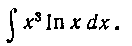

Решение. Имеем:

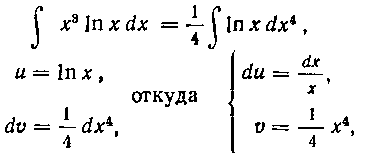
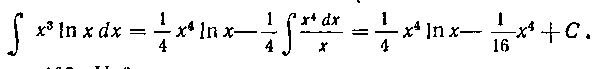
103. Найти интеграл:

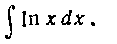
Решение. Имеем:

104. Найти интеграл:

105. Найти интеграл: 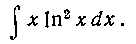Решение. Имеем:

Возьмем интеграл в правой части:

Окончательно получим:

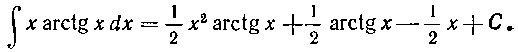
Интеграл в правой части берем опять по частям:

Теперь осталось перенести интеграл из правой части в левую, сделать затем в левой части равенства приведение подобных членов и разделить обе части равенства на полученный коэффициент: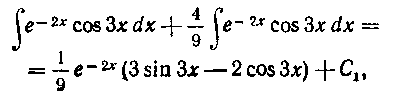

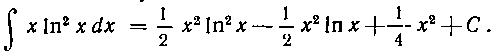
Необходимо обратить особое внимание на решение задач 106—108.

106. Найти интеграл:

•{см. решение примера 4 в п° 163 учебника). Решение. Проинтегрируем по частям:

Мы получили интеграл нисколько не проще заданного. Ho это не должно нас смущать. Проинтегрируем его еще раз по частям:

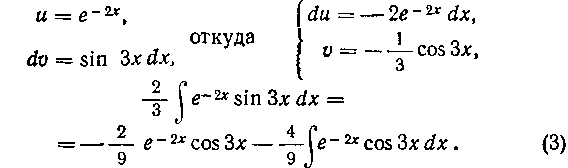
Подставив полученный результат в равенство (2), найдем:

или окончательно:

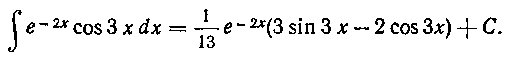
Замечание. При решении задачи 106мы могли бы с таким же успехом положить

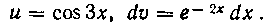
Ho в этом случае при вторичном интегрировании по частям следовало бы обязательно в качестве функции и выбрать тригонометрическую функцию.

Решите самостоятельно задачу 106 указанным вторым способом.

107. Найти интеграл:

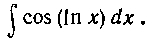
Решение. Поступаем аналогично решению задачи 106:

Интегрируем еще раз по частям:

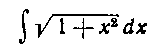
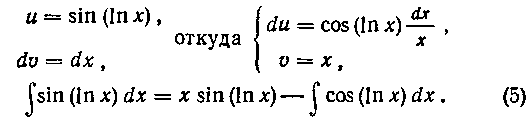
Объединяя равенства (4) и (5) и поступая аналогично решению задачи 106, окончательно получим:

108. Найти интеграл:

способом интегрирования по частям.

Решение. Первый способ. Интегрируем сразу по частям:

Преобразуем следующим образом интеграл в правой части (6):

Объединяя (6) и (7) и поступая аналогично решениям предыдущих двух задач, окончательно получим:

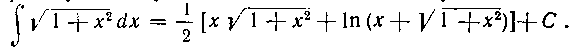
Второй способ. Освободимся от иррациональности в числителе, помножив и разделив подынтегральную функцию наА затем разобьем на 2 интеграла:

Полученный интеграл в правой части (8) возьмем по частям (поэтому мы и записали его в таком виде); именно, положим:

После двукратного интегрирования по частям мы снова вернулись к исходному интегралу. Объединяя равенства (8) и (9), получим:

*) Полученный интеграл легко берется подстановкой,

сравни с решением задачи 101.

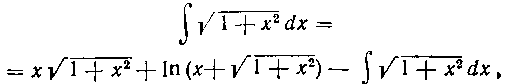
откуда окончательно получаем:

Задачи 1U9—12Ь решить способом интегрирования по частям.

Указание. В задаче 126 положитеИ затем после

интегрирования по частям преобразуйте интеграл

К виду

< Предыдущая		Следующая >