1.2. Способ замены переменной (способ подстановки)
Предварительно изучите по учебнику Г. М. Фихтен-гольца главу X, п° 160—161. Тщательно разберитесь в примерах, решенных в п° 161, и попробуйте примеры I—5 этого пункта решить введением под знак дифференциала (см. стр. 7). В примере 6 этого пункта учебника вы легко узнаете формулу 11 из нашей таблицы I.
Способ замены переменной или способ подстановки — один из наиболее сильных приемов интегрирования. К сожалению, нельзя дать общего ответа на вопрос: как выбрать удачную подстановку. В процессе решения задач укажем некоторые приемы для важных частных случаев.
Заместим, что способом подстановки в самых простейших случаях мы уже пользовались в § I при решении задач с применением правила III интегрирования и введением под знак дифференциала.
52. Найти интеграл:

Решение. Пробуем подстановку

Дифференцируя последнее равенство, получаем:

Заданный интеграл преобразуется теперь к табличному (см. формулу I, табл. I) и легко берется;
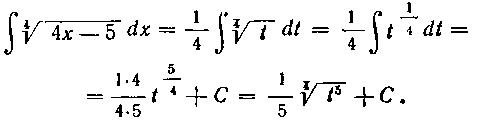
Возвращаясь теперь к первоначальной переменной х по формуле (I), находим:
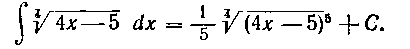
Мы могли бы здесь сразу воспользоваться правилом III.
Покажем, как с помощью подстановки берется интеграл  (см. выше задачу 8 на стр. 10). Берем подстановку
(см. выше задачу 8 на стр. 10). Берем подстановку Дифференцируя, получим
Дифференцируя, получим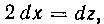 откуда
откуда Заданный интеграл примет вид:
Заданный интеграл примет вид:

Таким образом, если подынтегральная функция имеет вид f(ax-\-b), то удобна подстановка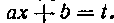
53. Найти интеграл:
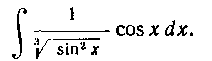
Решение. Возьмем подстановку  Дифференцируем это равенство:
Дифференцируем это равенство: 
Теперь наш интеграл примет вид:

Итак, с помощью подстановки Мы преобразовали
Мы преобразовали
заданный интеграл к табличному, который легко берется по формуле I таблицы I:
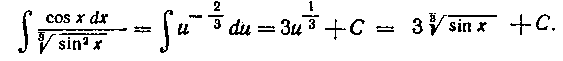
После интегрирования мы снова вернулись к первоначальному переменному х.
При решении задачи 53 можно рассуждать и так. В заданном интеграле, вводя множитель cos х под знак дифференциала (см. формулу 6 из табл. 2), получим:

Мы видим, что теперь под знаком интеграла все выражено через sin х и сама собой напрашивается подстановка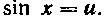
54. Найти интеграл:
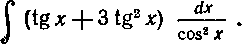
Решение. Берем подстановку  Дифференцируя, получим:
Дифференцируя, получим:
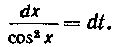
Заданный интеграл после этого берется до конца. В самом деле, имеем:
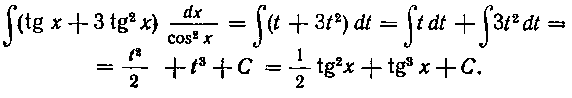
Здесь также можно было сначала подвести под дифференциал множитель (см. формулу 8 из табл. 2).
(см. формулу 8 из табл. 2).
Вели подынтегральное выражение можно разбить на два Сомножителя, в одном из которых довольно легко по таблице2 распознать дифференциал некоторой функции , а другой сомножитель после подстановки
, а другой сомножитель после подстановки Превращается в такую функцию
Превращается в такую функцию
от t, которую мы умеем интегрировать, то такая подстановка окажется удачной.
55. Найти интеграл:

Решение. В сомножителе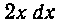 легко распознать дифференциал функции ‘
легко распознать дифференциал функции ‘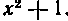 , Поэтому берем подстановку
, Поэтому берем подстановку
Отсюда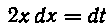 И
И Мы имеем:
Мы имеем:
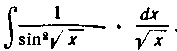

56. Найти интеграл:
Решение. В таблице 2 находим формулу 2'. Поэтому берем подстановку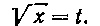
Отсюда
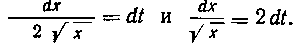
Итак,
57. Найти интеграл:

Решение. Формула 3 таблицы 2 подсказывает нам, что здесь полезна подстановка

В таблице I мы не находим подходящего интеграла. Поэтому пробуем применить еще подстановку, которая бы освободила подынтегральную функцию от радикала:

Наш интеграл примет вид:

откуда

Подставив все это в последний интеграл, получим:
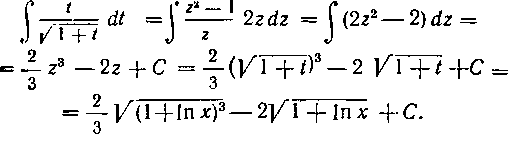
Мы после интегрирования вернулись сначала к переменной t, а затем к первоначальной переменной х.
Внимательно анализируя решение этой задачи, мы замечаем, что сразу пришли бы к цели, если бы воспользовались подстановкой

Рекомендуем читателю решить задачу 57 с помощью этой подстановки.
58. Найти интеграл:

Решение. Берем подстановку
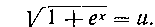
Выразим теперь dx через новую переменную и:

Итак,
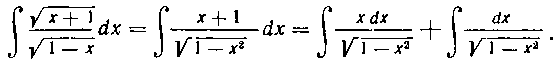
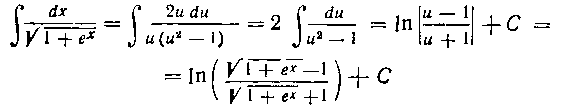
(см. формулу 12 из табл. I). 59. Найти интеграл:
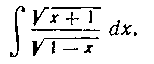
Решение. Освободимся от иррациональности в числителе, помножив числитель и знаменатель подынтегральной функции на ). Получим:
). Получим:
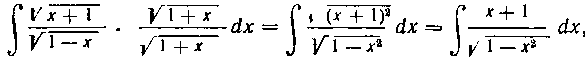
так как по условию I - f - х > 0.
Кажущееся сходство полученных двух интегралов обманчиво. Второй из них мы легко находим в таблице I (см. формулу 10 при а = I):

Первый интеграл берется подстановкой 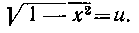 Дифференцируя, получим:
Дифференцируя, получим:

Следовательно,

Такой прием часто бывает очень полезен.
Таким образом, окончательно имеем:

60. Найти интеграл: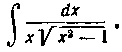
При решениизадач 52—60 мы обычно брали подстановку вида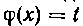 , т. е. мы какую-то функцию от х принимали за новую переменную. Иногда же бывают удобны подстановки вида
, т. е. мы какую-то функцию от х принимали за новую переменную. Иногда же бывают удобны подстановки вида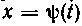 . Рассмотрим несколько задач, где удобно брать подстановки в такой форме. В задачах 61—63 мы применяем подстановки, называемые тригонометрическими подстановками.
. Рассмотрим несколько задач, где удобно брать подстановки в такой форме. В задачах 61—63 мы применяем подстановки, называемые тригонометрическими подстановками.
61. Найти интеграл: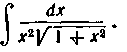
Решение. Здесь удобна подстановка
Решение. Берем подстановку Имеем:

Следовательно,

(где знак минус следует брать для *> 0).
так как она освобождает подынтегральную функцию от 20
радикала. В самом деле, имеем:
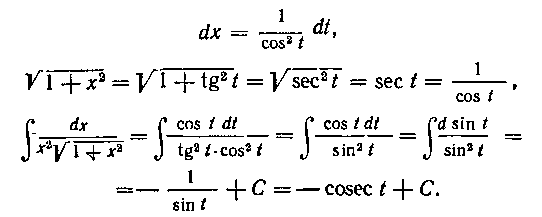
Чтобы вернуться к первоначальному переменному X9 нам остается выразить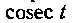 Через
Через Имеем:
Имеем:
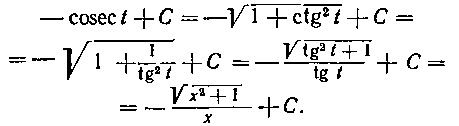
Попробуйте самостоятельно взять этот интеграл с по* мощью подстановки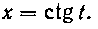
62. Найти интеграл:

Решение. Здесь удобна подстановка 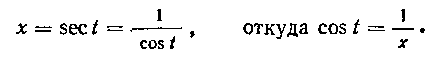 Далее имеем:
Далее имеем:
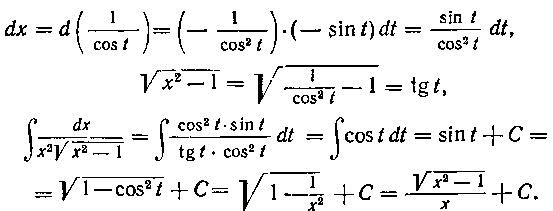
Попробуйте взять этот интеграл самостоятельно с помощью подстановки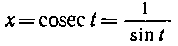
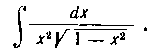
Решение. Здесь удобна подстановка  Имеем:
Имеем:
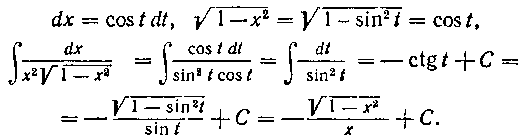
Попробуйте взять этот интеграл самостоятельно с помощью подстановки
Таким образом, если подынтегральная функция содержит радикал вида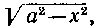 То удобны подстановки либо
То удобны подстановки либо . либо
. либо При радикалах вида
При радикалах вида  Удобны подстановки либо
Удобны подстановки либо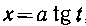 , либо
, либо  При радикалах вида
При радикалах вида Удобны подстановки либо
Удобны подстановки либо , либо
, либо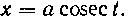
В задачах 64—90 найти интегралы, применяя подходящую подстановку.

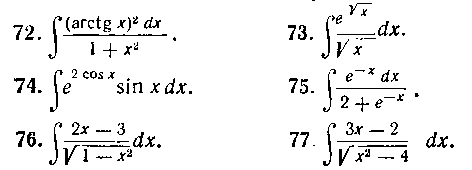
| < Предыдущая | Следующая > |
|---|