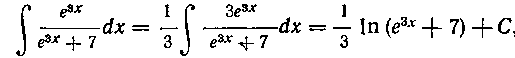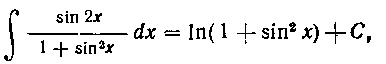1.1. Способ непосредственного интегрирования
Предварительно изучите по учебнику Г. М. Фихтенгольца «Основы математического анализа», т. I, главу X, п° 155—159. Обратите особое внимание на примеры, решенные в п° 159.
Способ непосредственного интегрирования опирается на таблицу основных интегралов и простейшие правила интегрирования.
Таблица I. Таблица основных интегралов
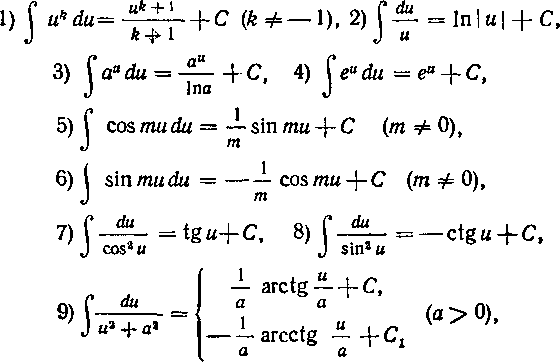
Все эти формулы справедливы независимо от того, является ли и независимой переменной, либо какой угодно функцией этой независимой переменной. По поводу формул 5), 6), 9), 11) и 12) смотрите учебник п° 159.
Простейшие правила интегрирования 
(здесь cl?*— постоянная величина,
~).
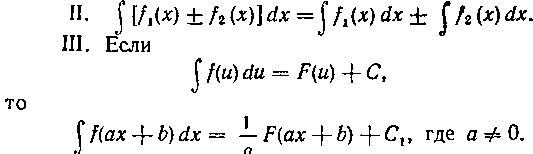
Очень часто встречаются случаи, когда с= I либо 6=0.
При отыскании неопределенных интегралов полезно помнить таблицу дифференциалов, но не в том виде, как она дана в учебнике (см. п° 91), а в немного преобразованном следующем виде (здесь как бы правые и левые части поменялись местами).
Таблица 2. Таблица дифференциалов
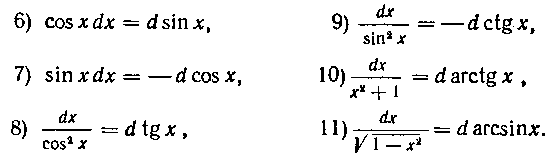
Этой таблицей мы в дальнейшем будем широко пользоваться. При этом представление, например, выражения
в виде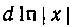
Или выражения
В виде 
Мы будем называть подведением функций соответ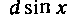
ственно
Или
Под знак дифференциала.
I. Найти интеграл:
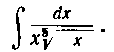
Решение. Записываем подынтегральную функцию в виде степени с отрицательным дробным показателем и применяем формулу I из таблицы I:
2. Найти интеграл:
Решение. Числитель подынтегральной функции делим почленно на знаменатель. Затем применяем правила
II, I и формулу I из таблицы I:
Решение. Возводим числитель в квадрат и делим почленно на знаменатель. Далее поступаем, как в задаче 2:
4. Найти интеграл:
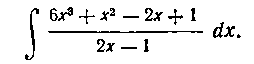
Решение. Сначала исключаем целую часть рациональной дроби, деля числитель на знаменатель. Имеем:
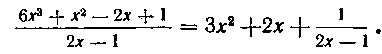
Применяя теперь правило II, получим:
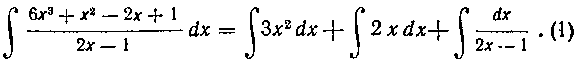
Первые два интеграла правой части (I) вычисляются по формуле I из таблицы I:
К третьему же интегралу правой части применяем правило III интегрирования. В нашем случае
Поэтому на основании формулы 2 из таблицы I имеем:
Итак:
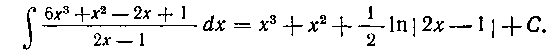
Укажем другой способ рассуждений при вычислении третьего интеграла в правой части равенства (I).
*) Произвольную постоянную мы учтем позднее при написании окончательного ответа. Мы будем поступать так и в дальнейшем.
Легко видеть, что
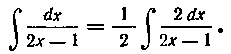
Интеграл не изменился, так как мы подынтегральное выражение помножили на 2 и одновременно интеграл разделили на 2. Если мы теперь множитель 2 при dx подведем под знак дифференциала (см. формулу I из табл. 2), то получим:
где и = 2х—I. Мы получили табличный интеграл (см. формулу 2 из табл. I).
Итак, окончательно
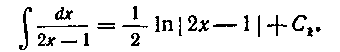
Замечание. Если подынтегральная функция представляет собой рациональную дробь, у которой степень многочлена числителя больше или равна степени многочлена знаменателя, то прежде всего следует исключить целую часть путем деления числителя рациональной дроби на знаменатель.
5. Найти интеграл:
ся
Решение. Освобождаемся от иррациональности в знаменателе:
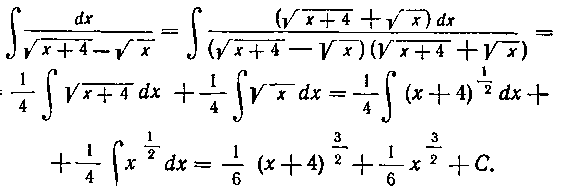
Мы воспользовались здесь правилом III и формулой I из таблицы I.
6. Найти интеграл:
Решение. Имеем:
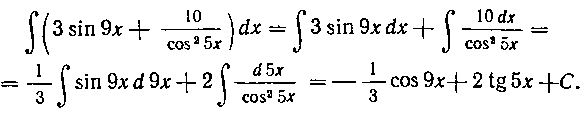
Мы использовали здесь правило II; подведением соответствующего постоянного множителя под знак дифференциала мы привели интегралы к табличным (см. формулы 6 и 7 из табл. I).
7. Найти интеграл: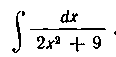
Решение. Чтобы свести данный интеграл к табличному (см. формулу 9 из табл. I), достаточно подвести под дифференциал множитель
И разделить весь интеграл на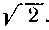
Тогда, сравнив полученный интеграле формулой 9, увидим, что
А = 3. Следовательно, получим:
Замечание. Совершенно аналогично следует поступать с интегралами вида
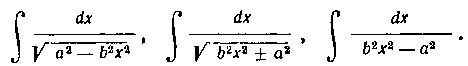
Если в каждом из них мы введем под дифференциал множитель b и разделим интеграл на этот множитель, то приведем данные интегралы к табличным (см. формулы 10, 11, 12 в табл. I), причем и = Ьх.
8. Найти интеграл:
Решение. Вряд ли кому-нибудь придет в голову мысль возвести данный двучлен в 27-ю степень и затем интегрировать сумму из 28-ми слагаемых, хотя такой путь вполне законен. Данный интеграл берется совсем легко с помощью правила III и формулы I из таблицы I. В самом деле, имеем:
Способ непосредственного интегрирования дает возможность брать интегралы вида
Данный интеграл можно свести к табличному, если ввести множитель 2 под дифференциал и разделить весь интеграл на 2:
где
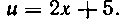
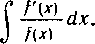
В самом деле, так как f'(x)dx =Af (х), то
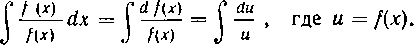
Окончательно имеем:
Итак, если числитель подынтегральной функщш равен производной ее знаменателя (или отличается от нее постоянным множителем), то интеграл равен логарифму модуля знаменателя плюс произвольная постоянная.
Рассмотрим несколько задач.
9. Найти интеграл: так как функция cos л: в числителе есть производная знаменателя sin х.
Решение. Имеем:
Применяя к равенству (2) правило III, мы легко возьмем и более сложный интеграл:
10. Найти интеграл:
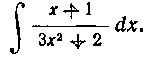
Решен ие. Имеем:
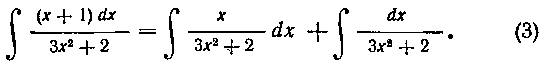
Так как производная знаменателя равна 6*, то достаточно в первом интеграле помножить числитель на 6, а весь интеграл разделить на 6:
Второй интеграл равенства (3) берется аналогично интегралу задачи 7:
Окончательно получим:
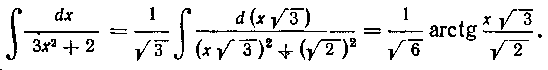
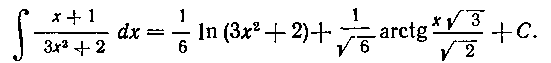
так как после умножения числителя на 3 он стал равен производной знаменателя.
так как числитель подынтегральной функции равен производной знаменателя.
В задачах 13—26, пользуясь формулами таблицы I и правилами интегрирования I и II, найти заданные интегралы.
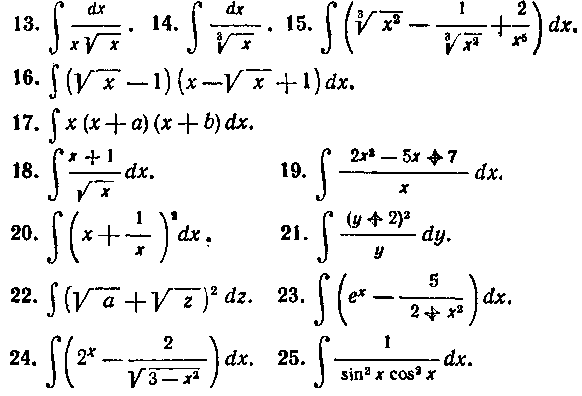
Указание. В задаче 25 числитель I подынтегральной функции замените по формуле I = sin2 х 4- cos8 х и разделите почленно на знаменатель. В задаче 26 воспользуйтесь формулой cos 2;r = cos8 х — — Sin2X и разложите на множители.
В задачах 27 — 30 найти интегралы, предварительно исключив целую часть рациональной дроби.
В задачах 29—41, пользуясь правилом интегрирования III или подведением под знак дифференциала, найти заданные интегралы. 
При решении задач 42—47 посмотрите решения задач 9—12.
Указание. При решении задачи 43 воспользуйтесь указанием к задаче 25.
В задачах 48, 49 подведите предварительно числитель подынтегральной функции под знак дифференциала.
В задачах 50, 51 подведите предварительно множители х, х% под знак дифференциала.
| Следующая > |
|---|
