Решение типовых задач контрольной работы по разделам 1 и 2
Тема «Функции нескольких переменных» будет рассмотрена после определенного интеграла.
1.1.1. Выполнить действия
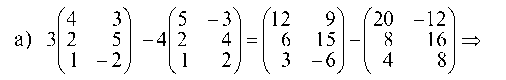
Сначала умножаем матрицу на число, а затем вычитаем из одной матрицы другую
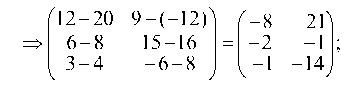
б) нужно перемножить две матрицы: С = AS. Это возможно в случае, если число столбцов матрицы А равно числу строк матрицы S. Элемент Cjk матрицы С имеет вид:
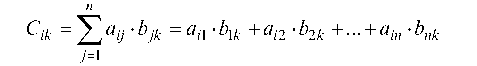
(г = 1, 2, ..., и; к = 1, 2, ..., и), т. е. элемент матрицы С, стоящей в г-й строке и к-м столбце, равен сумме произведений соответственных элементов г-й строки матрицы А и к-го столбца матрицы S.
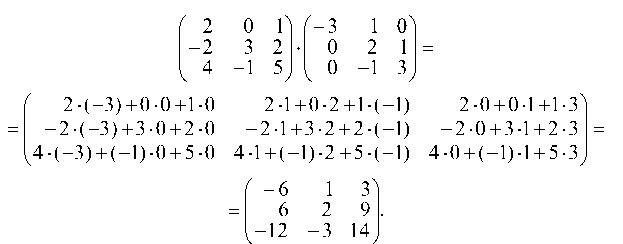
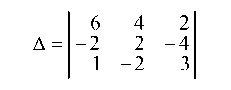
Справа от определителя приписываются два первых столбца, берутся со знаком «+» три произведения элементов, стоящих на главной диагонали и двух диагоналях ей параллельной и со знаком минус три произведения элементов, стоящих на побочной диагонали и двух диагоналях ей параллельной;
б) разложением по строке.
Определитель D равен сумме произведений всех элементов произвольной его строки на их алгебраические дополнения
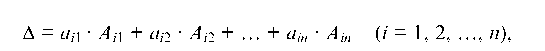
где Aj — алгебраическое дополнение элемента определителя Яу, равное
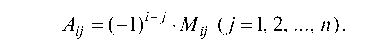
1.2.1. Убедимся, что определитель D равен нулю
а) по определению (одной из схем):
©
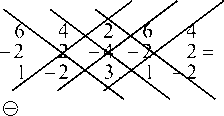
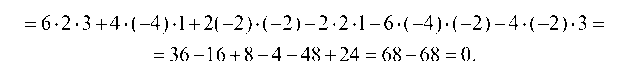
Здесь Mj — минор элемента Яу, т. е. определитель (n - 1)-го порядка, получающийся после вычеркивания из определителя n-го порядка i-й строки и у-го столбца.
Вычисляем определитель D разложением по элементам первой строки
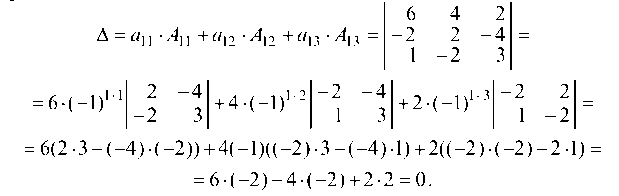
1.3. Обратная матрица
1.3.1. Найти обратную матрицу к матрице А и проверить выполнение равенства А ¦ A1 = £:
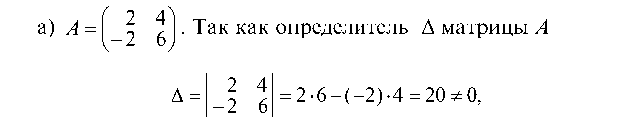
то матрица А является невырожденной и для нее существует об-
ратная матрица А 1.
Находим алгебраические дополнения для определителя Д:
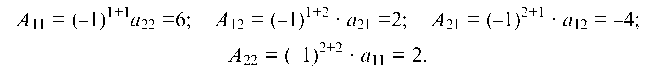
Составляем матрицу из этих алгебраических дополнений и транспонируя ее, получаем присоединенную матрицу (А*):
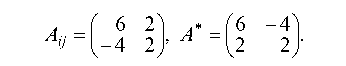
-1
Вычисляем обратную матрицу А
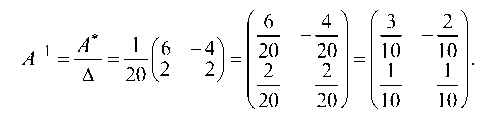
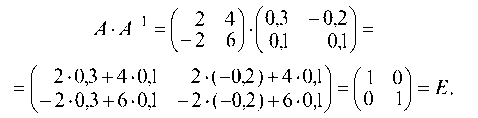
Так как А ¦ А 1 = то обратная матрица найдена правильно;
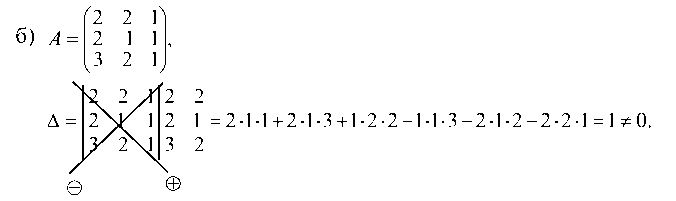
Находим алгебраические дополнения
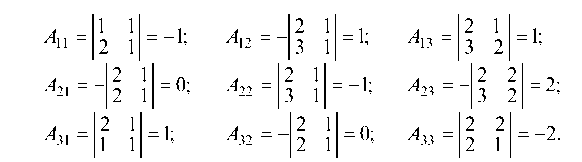
Определяем
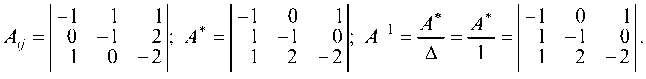
Проверяем
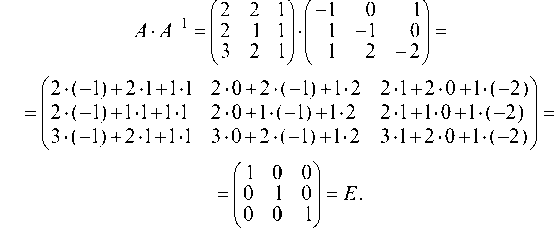
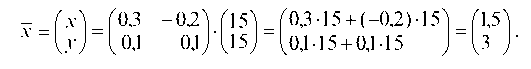
Отсюда: х = 1,5; у = 3.
1.4.1. Записать систему в матричном виде Ах = b :
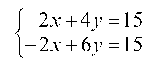
и решить ее средствами матричного исчисления.
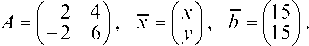
Решение этой системы через обратную матрицу А 1 имеет вид
х = А 1 • b.
В пункте 1.3.1: а) была найдена обратная матрица А 1, тогда
Можно сделать проверку, т. е. подставить найденные значения х и у в исходную систему уравнений.
1.4.2. Решить систему методом исключения переменных (методом Гаусса):
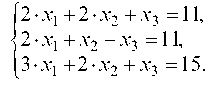
Выберем в качестве первого ведущего уравнения — первое уравнение системы и оно в дальнейшем остается без изменения, а в качестве первого ведущего неизвестного — хь
Исключаем неизвестную х1 из второго и третьего уравнений системы с помощью первого уравнения. Для этого из 1-го уравнения вычитаем второе, получим х2 + 2х3 = 0, затем 1-ое уравнение умножаем на 3, а 3-е уравнение — на 2 и вычитаем из одного другое, получим 2х2 + х3 = 3.
Выписываем систему
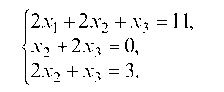
Неизвестная х1 исключена. Первый шаг закончен. Теперь второе уравнение берется за ведущее и оно в дальнейшем не изменяется, а за ведущую неизвестную принимается х2. Исключаем из 3-го уравнения х2, для этого 2-ое уравнение умножаем на 2 и вычитаем из него 3-е уравнение системы, получаем 3х3 = -3.
Получим систему
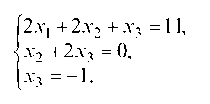
Прямой ход метода Гаусса закончен. Обратным ходом получаем:
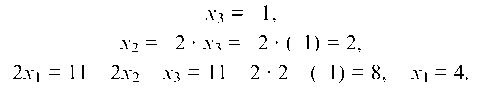
Итак, х1 = 4, х2 = 2, х3 = -1.
1.4.3. Дана система
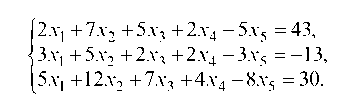
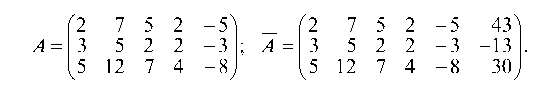
Рассмотрим минор 2-го порядка
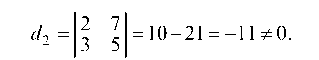
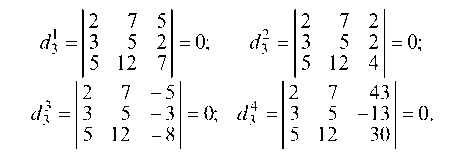
Так как миноры d^, и d| равны нулю, то ранг системы
равен двум, а так как минор = 0, то и ранг расширенной матрицы равен двум. Равенство рангов расширенной матрицы и матрицы системы на основании теоремы Кронекера—Капелли говорит о том, что система алгебраических уравнений совместна, т. е. имеет решение.
2. Найти общее решение системы в виде
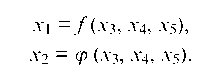
Так как число неизвестных пять, а ранг матрицы равен двум, то разность между ними, равная трем (n - r = 5 - 2 = 3), говорит
о том, что три неизвестных будут свободными, пусть это будут x3, x4, x5.
Берем первые два уравнения системы и записываем их относительно x1 и x2 (коэффициенты при этих неизвестных составляют минор 2-го порядка отличный от нуля), а неизвестные x3, x4, x5 переносим в правую часть:
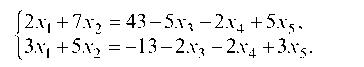
Имеем систему двух уравнений с двумя неизвестными x1 и x2. Умножая первое уравнение на 5, а второе на 7 и вычитая одно из другого, найдем x1 и подставляя его в 1-ое уравнение, после преобразований получим выражение для x2:
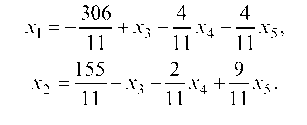
3. Найти частное решение системы a = (х1, х2, х3, х4, х5), положив х3 = 5, х4 = 2, х5 = 3 и проверить систему.
Находим х1 и х2:
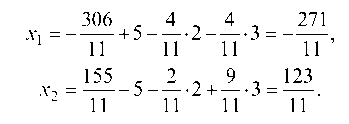
Следовательно, частное решение имеет вид:
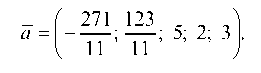
Подставляем в исходную систему значенш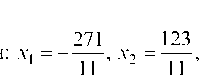
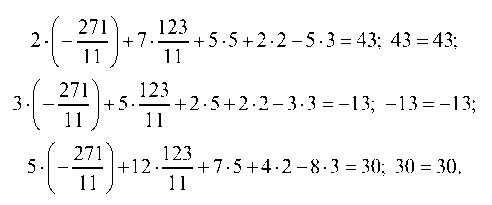
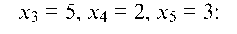
Выполнение тождества для всех уравнений системы говорит о том, что вектор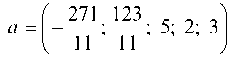
Является частным реше
нием исходной системы уравнений.
1.5. Собственные числа и собственные векторы
1.5.1. Найти собственные числа и соответствующие им собственные векторы для матрицы
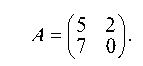
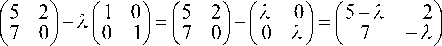
или
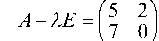
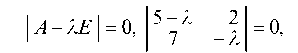
отсюда (5 - 1) ¦ (-1) - 2 ¦ 7 = 0, или I2 - 51 - 14 = 0. Корни этого уравнения 1 = -2 и 12 = 7 и являются собственными числами.
Для отыскания собственных векторов используем систему уравнений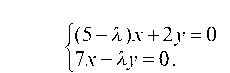
Полагая 1 = 11 = -2, получаем систему уравнений для первого собственного вектора U(M1, M2):
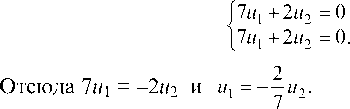
Следовательно, первым собственным вектором, определяющим первое собственное направление, является
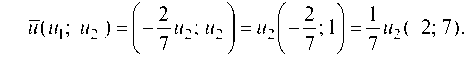
Меняя M2, будем получать различные векторы, лежащие на одной прямой (коллинеарные). Все они — собственные.
Полагая 1 = 12 = 7, получаем систему уравнений для отыскания координат второго собственного вектора V (V1; v2):
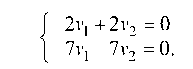
Отсюда v1 = v2 — общее решение (v2 — свободная, v1 — базисная переменная).
Второй собственный вектор V(V1; v2) = (v2; v2) = V2 (1; 1) определяет второе собственное направление.
2. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ. 2.1. Прямая линия на плоскости2.1. Прямая линия на плоскости
2.1.1. На прямую /: 3x + 2y - 12 = 0, которая способна отражать лучи, падает луч, заданный уравнением I1: 3x + 4y - 18 = 0. Составить уравнение отраженного луча.
Решение. Так как угол падения луча равен углу отражения луча, то Zj = Z j2, т. е. tg j1 = tg j2 (рис. 31).
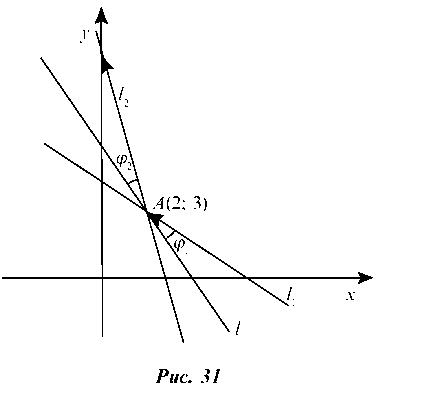
Уравнение отраженного луча — прямой /2 — ищем в виде: y - yA = k2(x - xa).
Для нахождения координат точки А решим систему уравнений: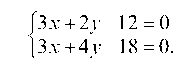
Вычитая, найдем: -2у + 6 = 0, у = 3 и 3x = 12 -2у = 12 - 2 ¦ 3 = 6, x = 2, т. е. xA = 2 и yA = 3.
Найдем угловые коэффициенты прямых / и /1:
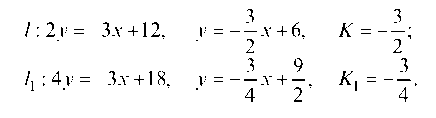
Запишем тангенс угла между прямыми / и /1:
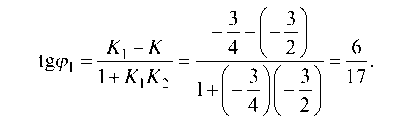
Для нахождения углового коэффициента прямой /2 запишем тангенс угла между прямыми / и /2 и учтем, что tg Р1 = tg (pi-
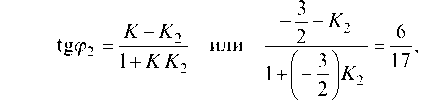
далее
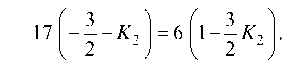
Отсюда Т огда искомое уравнение отраженного луча
имеет вид:
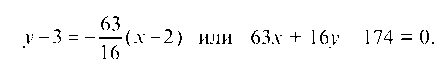
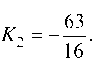
2.1.2. Дан треугольник АВС с вершинами А(5; 6), B(4; -5), C(-4; 5) (рис. 32).
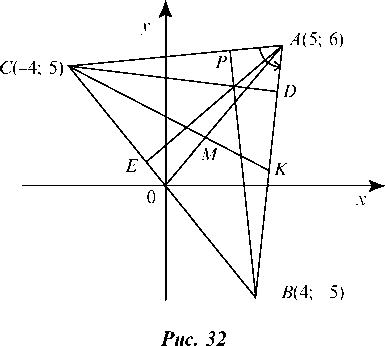
Найдем уравнения всех сторон треугольника и их угловые коэффициенты.
Уравнение прямой AS:
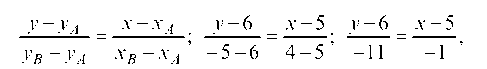
отсюда 11 ¦ х - у - 49 = 0 или у = 11х - 49 и угловой коэффициент прямой AS равен: Kab = 11.
Уравнение прямой AC:
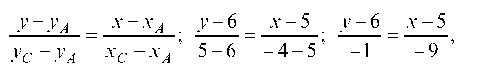
отсюда
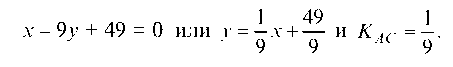
Уравнение прямой SC: отсюда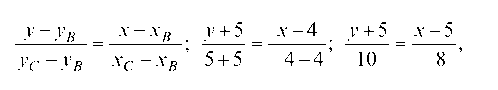
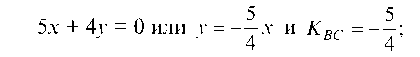
а) вычислим величину внутреннего угла А треугольника:
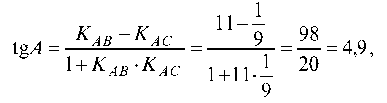
отсюда ZA = 78°27'55" = 1,37 (с точностью до 0,01) радиан;
б) найдем точку M пересечения медиан.
Определяем координаты точек K и O, делящих стороны AS и SC попалам:
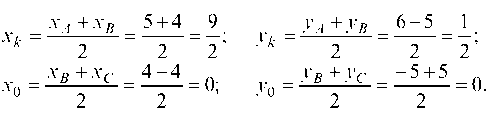
Уравнение медианы CK:
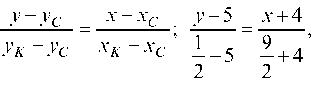
отсюда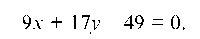
Уравнение медианы AO:
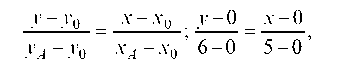
отсюда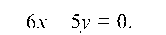
Решая систему уравнений, описывающих медианы CK и AO, найдем координаты точки M:
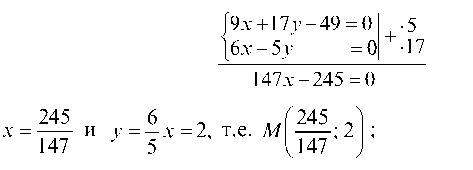
в) находим точку Р пересечения высот CD и AE.
Уравнение высоты CD ищем в виде: y - yC = KCD(x - xC) и так как прямая CD L прямой AS, то
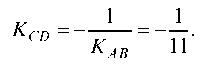
Тогда
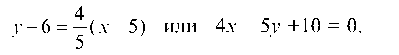
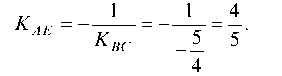
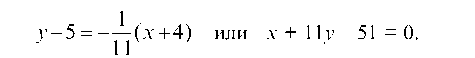
Уравнение высоты AE берем в виде: y - yA = KAE(x - xA) и так как прямая AE L прямой SC, то
Тогда
г) определяем длину высоты треугольника А£, опущенной из вершины А на сторону SC, для чего запишем нормальное уравнение прямой SC:
е) находим систему линейных неравенств, определяющих внутреннюю область треугольника ASC вместе с границами.
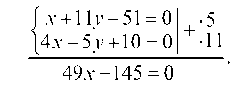
Отсюда
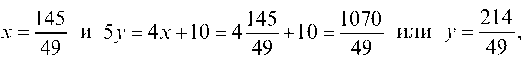
т. е.
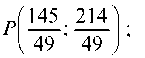
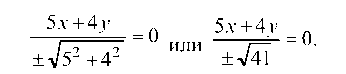
Тогда длина высоты А£ равна:
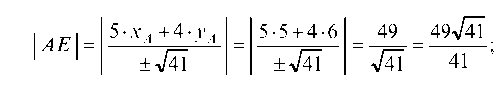
д) площадь треугольника найдем по формуле:
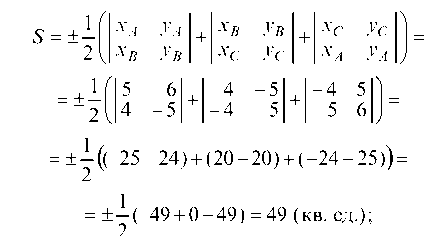
Имеем: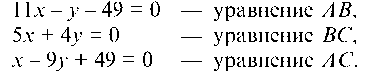
Берем любую точку, лежащую внутри треугольника ASC, например, точку (1; 1) и подставляем ее координаты в левую часть уравнений сторон: 11 ¦ 1 - 1 - 49 = -39 <0; 5 ¦ 1 + 4 ¦ 1 = 9 > 0;
1 - 9 ¦ 1 + 49 = 41 > 0, следовательно, система неравенств имеет вид: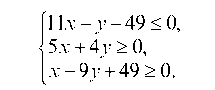
| < Предыдущая | Следующая > |
|---|
