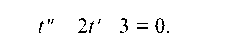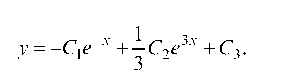Решение типовых задач контрольной работы по разделам 3, 4 и 5 4. Интегральное исчисление
4.1.1. Найти интегралы и в пункте а) результат проверить дифференцированием:
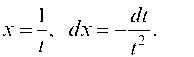
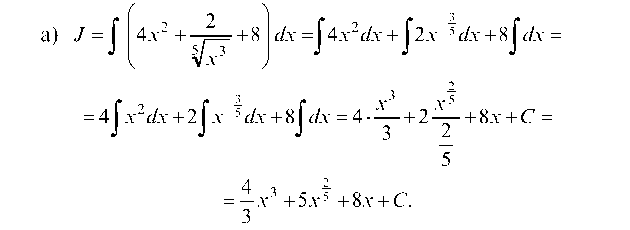
Результат проверяем дифференцированием:
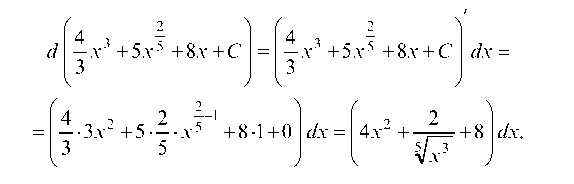
Верно.
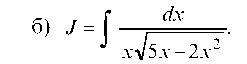
Введем подстановку
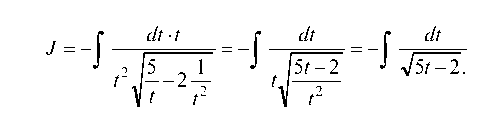
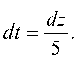
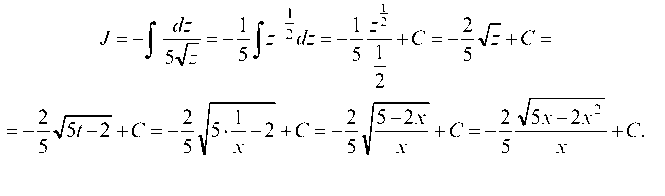
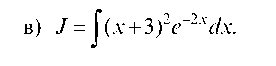
Применяем формулу интегрирования по частям:
Пусть
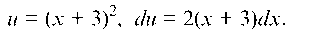
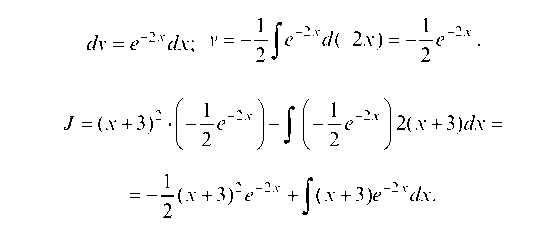
Еще раз интегрируем по частям: и = x + 3, du = dx.
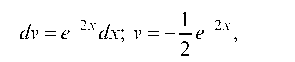
тогда
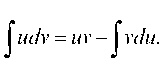
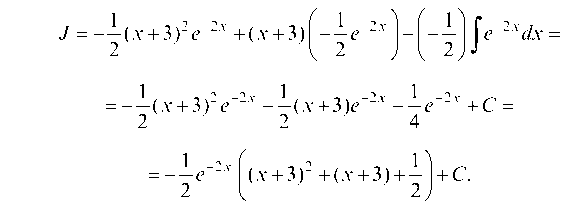
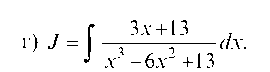
Подинтегральная функция представляет собой правильную алгебраическую дробь. Раскладываем знаменатель на простые множители и дробь представляем в виде суммы элементарных дробей:
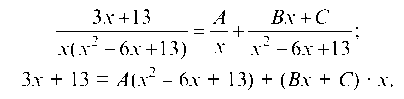
3х + 13 = А + Вх + С ; х(х2 - 6х +13) х х2 - 6х +13 3х + 13 = А(х2 - 6х + 13) + (Вх + С) • х.
Равенство справедливо при любом х. Пусть
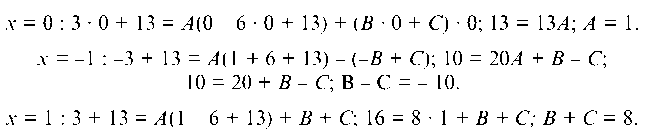
х = 0 : 3 • 0 + 13 = А(0 - 6 • 0 + 13) + (В • 0 + С) • 0; 13 = 13А; А = 1.
х = -1 : -3 + 13 = А(1 + 6 + 13) - (-В + С); 10 = 20А + В - С;
10 = 20 + В - С; В - С = - 10.
х = 1 : 3 + 13 = А(1 - 6 + 13) + В + С; 16 = 8 • 1 + В + С; В + С = 8. Гв - С = -10

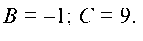
Имеем систему: [В + С = 8 , из которой В = -1; С = 9.
Тогда
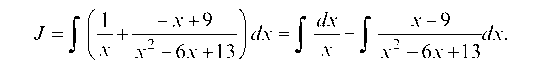
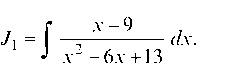
Рассмотрим /1 = Я
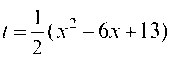
1 2
Пусть г = ^(х -6х + 13), отсюда Л = (х - 3)^х. Имеем
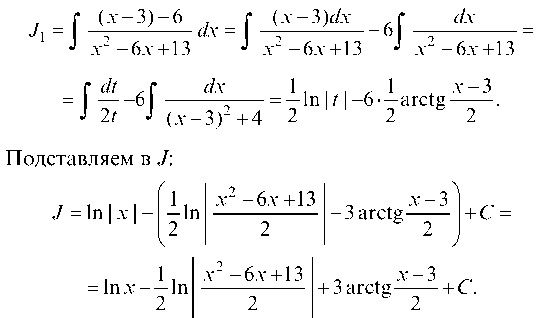
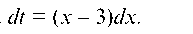
х х - 6х +13 х - 9
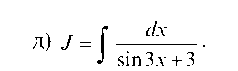
Пусть

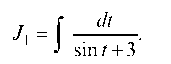
Рассмотрим
Имеем:
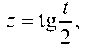
Введем подстановку: тогда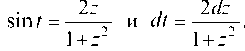

4.2.1. Вычислить интегралы или установить их расходимость:
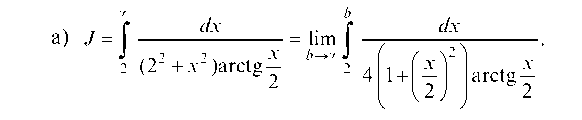
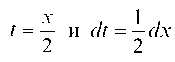
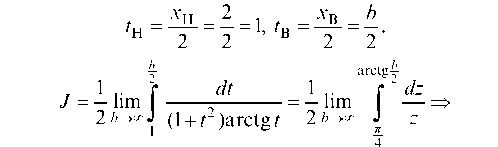
Пусть z = arctg t, тогда
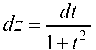
и новые пределы интегриро-
вания будут:
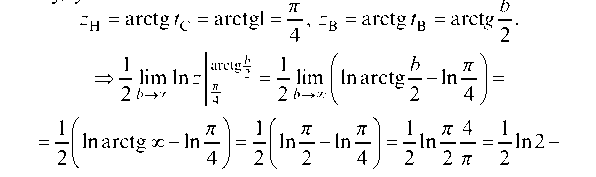
интеграл сходится.
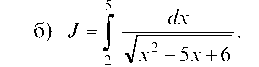
Найдем точки, в которых подинтегральная функция терпит разрыв: x2 - 5x + 6 = 0, x1 = 2, x2 = 3 и обе точки принадлежат отрезку интегрирования [2; 5]. Тогда
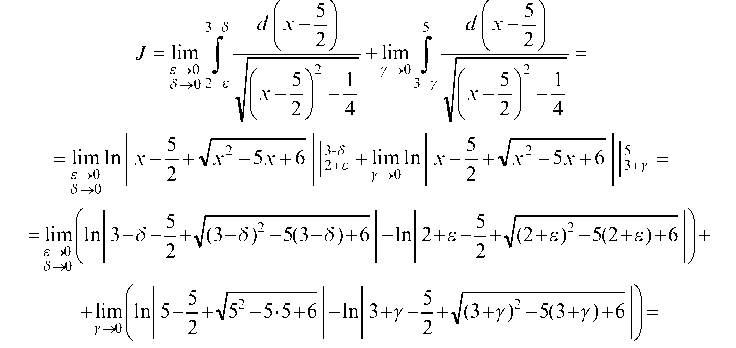
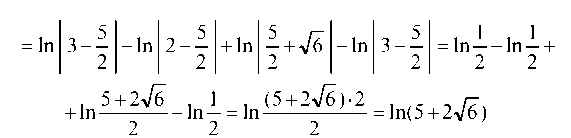
интеграл сходится.
4.3. Приложения определенных интегралов
4.3.1. Найти площадь фигуры, ограниченной линиями, и построить схематические чертежи фигур.
а) у = x2 + 2x - 16, 4x - y - 8 = 0.
Имеем параболу: y = (x + 1)2 - 17 и прямую: 4х - у - 8 = 0. Нужно определить заштрихованную площадь (рис. 53).
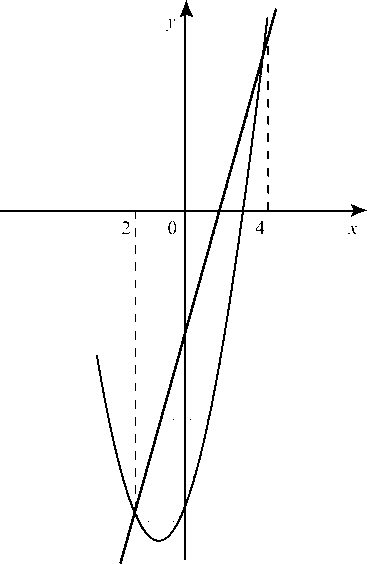
Найдем общие точки фигуры (пределы интегрирования):
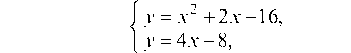
2
отсюда х2 - 2х - 8 = 0 и х1 = -2, х2 = 4. Площадь фигуры определяется как:
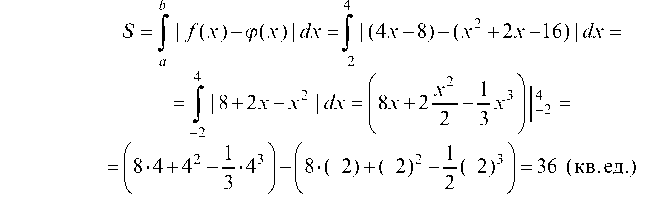
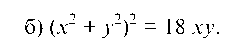
Запишем это уравнение в полярной системе координат:
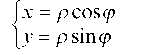
Подставив, получим:
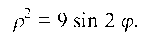
Площадь лемнискаты (рис. 54) равна четырем заштрихованным площадям, тогда

4.3.2. Найти объем тела вращения вокруг оси Ох фигуры, ограниченной линиями:
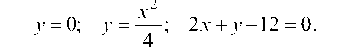
Находим общие точки фигуры: отсюда

Заштрихованная фигура (рис. 55) вращается вокруг оси Ох. Объем тела вращения определяется как:
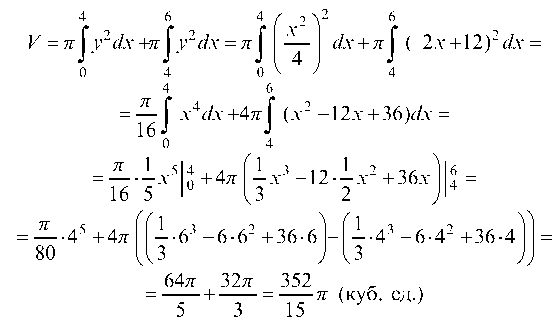
4.4. Приближенные вычисления определенных интегралов
4.4.1. Разбивая отрезок интегрирования сначала на 10 равных частей, а затем на 20 частей, найти приближенно интегралы и J20. Определить точность с помощью разности

а) по формуле трапеций;
б) по формуле Симпсона.
Решение. Имеем подинтегральную функцию ставим вспомогательную таблицу.

а) По формуле трапеций.
При делении на 10 частей:
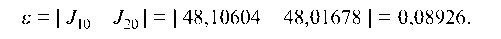
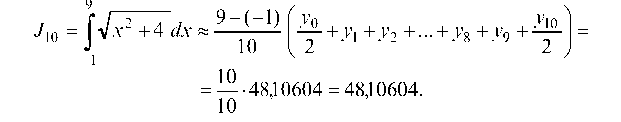
При делении на 20 частей:
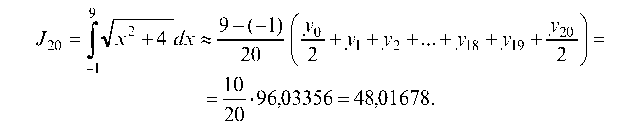
Точность вычислений оцениваем с помощью разности:
б) По формуле Симпсона.
При делении на 10 частей:
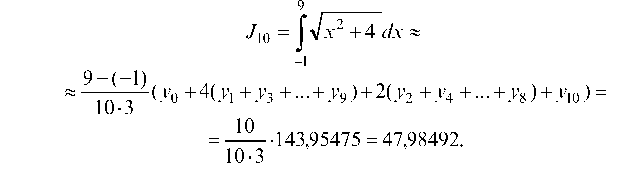
При делении на 20 частей:
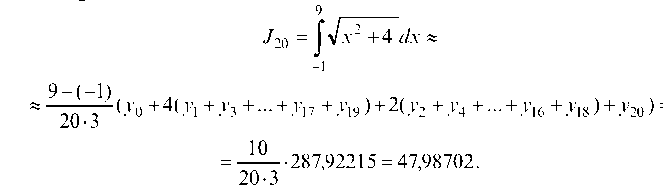
Точность вычислений: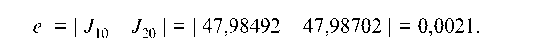
Известно, что при одинаковом числе точек разбиения формула Симпсона дает более точный результат.
5. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
5.1. Частные производные и дифференциал функции5.1.1. Найти частные производные zx, z'y, и z" функций:
“У ~xy
а) z = (x - 4)2у2 + x4(y + 2)3 + 8.
Находим:
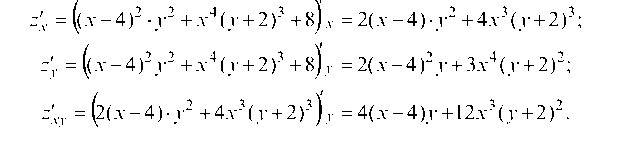
Полный дифференциал определяется как:
Находим:
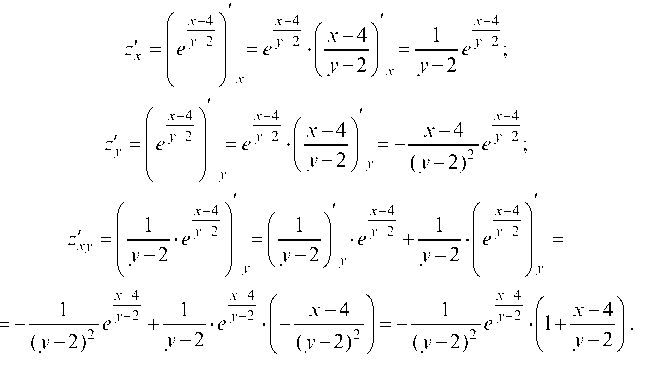
5.1.2. Найти дифференциал dz функции:
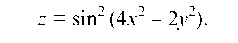
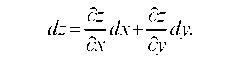
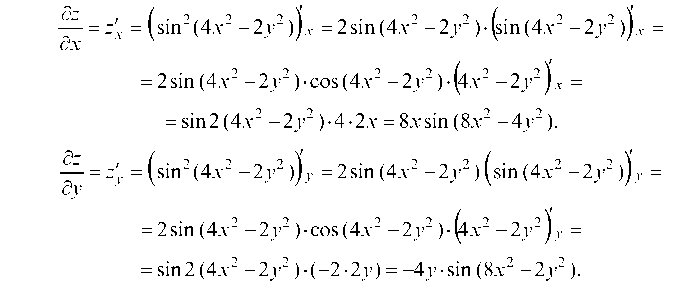
Тогда полный дифференциал будет равен:
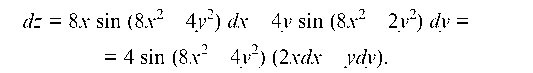
22
5.1.3. Показать, что функция z = у In (4x - 2у ) удовлетворяет уравнению
Найдем частные производные:
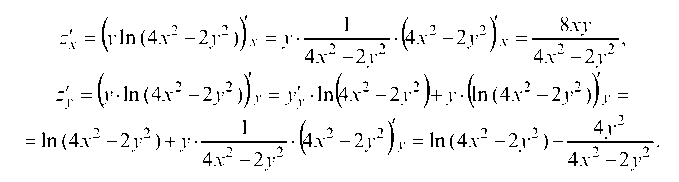
Подставляем найденные частные производные в уравнение:
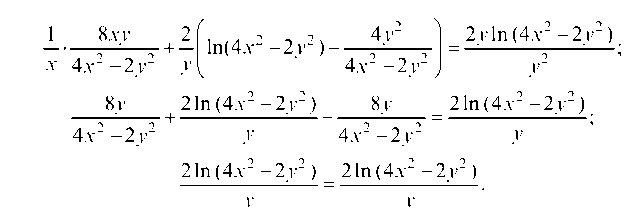
Получили тождество.
5.2.1. Составить уравнение касательной плоскости и уравнение нормали к поверхности 4z = xy - 2x - 4y + 8 в точке M (-4; -2; 8).
Решение. Проверим принадлежит ли точка M поверхности:

следовательно, точка M принадлежит поверхности.
Уравнение касательной плоскости имеет вид:

Найдем значения частных производных в точке M:
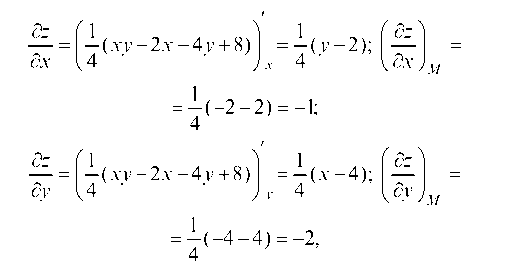
и подставим в уравнение касательной плоскости:
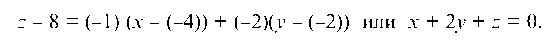
Уравнение нормали берем в виде:
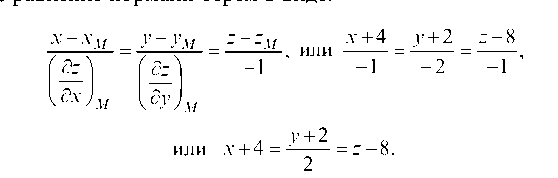
5.2.2. Найти градиент и производную по направлению a = 4i -2j
22
функции z = In (4x + 2y ) в точке A (-2; 4).
Решение. Градиент функции z = f (x, y) равен:

Тогда градиент в точке A равен:
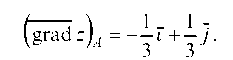
Производная функции z в направлении вектора а вычисляется по формуле:
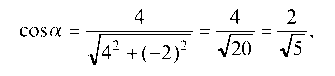


Найдем частные производные:

и их значения в точке A (-2; 4):
Найдем направляющий косинус вектора а : тогда
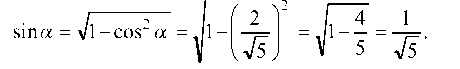
Следовательно,
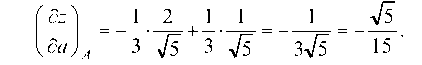
5.2.3. Найти наибольшее и наименьшее значения функции 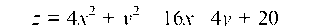 в замкнутой области D, заданной неравенствами:
в замкнутой области D, заданной неравенствами:
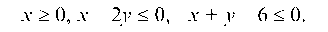
Решение.
а) Найдем частные производные и приравняем их к нулю (необходимые условия экстремума):
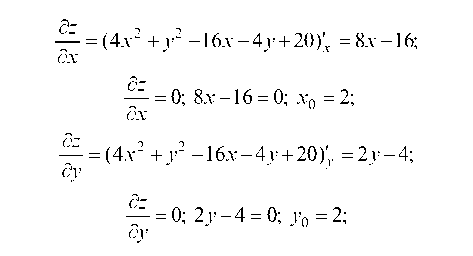
Стационарная точка x0 = 2, y0 = 2 лежит в замкнутой области, так как: 2 > 0; 2 - 2 ¦ 2 < 0; 2 + 2 - 6 < 0.
Найдем вторые частные производные:
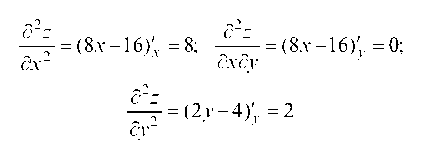
и их значения в стационарной точке M (2; 2):

Так как D = A ¦ C - B2 = 8 ¦ 2 - 0 = 16 > 0, то в точке M функция имеет экстремум, а именно минимум, так как А = 8 > 0; zmin (2; 2) = 4 ¦ 22 + 22 - 16 ¦ 2 - 4 ¦ 2 + 20 = 0.
Рассмотрим контур х = 0 (прямая OA). Имеем функцию одной переменной: z = y2 - 4y + 20. Исследуем ее на экстремум:
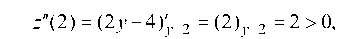
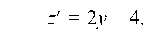
Из z' = 0 имеем 2y - 4 = 0 или y = 2. И так как
2
то имеем минимум и zC = z (2) = 2 - 4 ¦ 2 + 20 = 16.
Далее рассмотрим контур х + y - 6 = 0 или y = 6 - х (прямая AB). Имеем:
или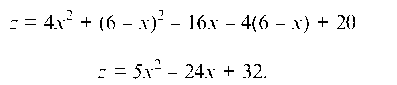
Найдем z' = 10х - 24 и из z' = 0 имеем 10х - 24 = 0, или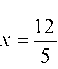 Так как z" = (10х - 24)' = 10 > 0, то при
Так как z" = (10х - 24)' = 10 > 0, то при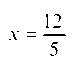 Имеем минимум и
Имеем минимум и
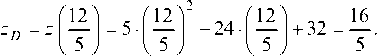
На контуре х - 2у = 0 или х = 2у (прямая OB) имеем z = 4(2y)2 + y2 - 16 ¦ 2y - 4y+ 20 или z = 17y2 - 36y + 20. Находим производную z' = (17y2 - 36y + 20)' = 34y - 36, приравниваем ее
к нулю z' = 0 или 34y - 36 = 0, отсюда
Так как z " = (34y - 36)' = 34 > 0, то в точке Имеем мини
Имеем мини
мум и
Найдем значения функции z в точках O (0; 0), A (0; 6) и B (4; 2):
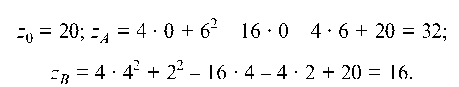
Из найденных значений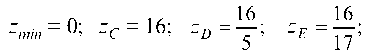
z0 = 20; zA = 32; zB = 16 выбираем наименьшее и наибольшее. Получаем что zHattu = ° zHauG = 32.
8. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
8.1. Уравнения первого порядка
8.1.1. Найти общее решение уравнения:
а) у' = e4x - 2y. Это дифференциальное уравнение первого порядка с разделяющимися переменными. Решаем его.
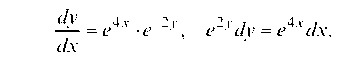
Интегрируем
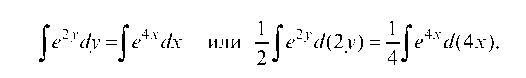
Тогда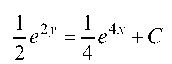 Или
Или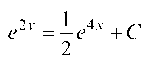 Есть общее реше
Есть общее реше
ние исходного уравнения.
получили однородное дифференциальное уравнение первого порядка, которое сведем к уравнению с разделяющимися переменными введением функции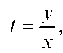 Отсюда y = x ¦ t и у' = t + x ¦ t'. Подставляем в исходное уравнение (3 - 5t)(t + xt') = 5 + 3t,
Отсюда y = x ¦ t и у' = t + x ¦ t'. Подставляем в исходное уравнение (3 - 5t)(t + xt') = 5 + 3t,
или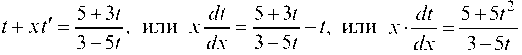 . Разде
. Разде
ляем переменные Числитель делим почленно на зна
Числитель делим почленно на зна
менатель и интегрируем
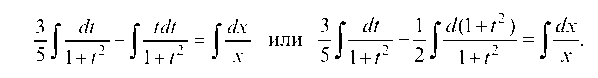
Все интегралы табличные, тогда 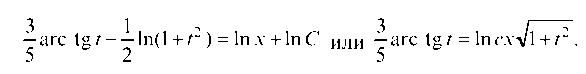 Подставляем сюда
Подставляем сюда Получим
Получим
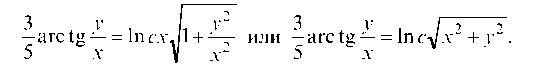
Это и будет общее решение исходного дифференциального уравнения.
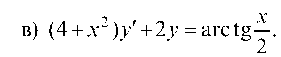
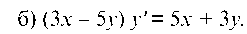
Разделив уравнение на х
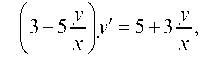
Это линейное дифференциальное уравнение первого порядка, которое решаем подстановкой Бернулли y = и (x) ¦ v (x) и у' = и' v + uV, после чего приходим к решению двух дифференциальных уравнений с разделяющимися переменными.
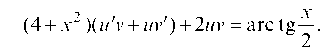
Группируем
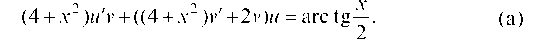
Пусть
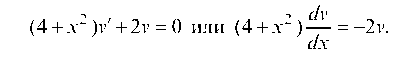
Разделяем переменные и интегрируем отсюда
Подставляем функцию (b) в уравнение (а)
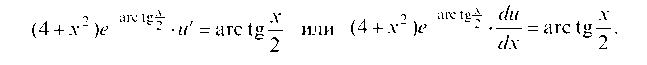
Разделяем переменные и интегрируем
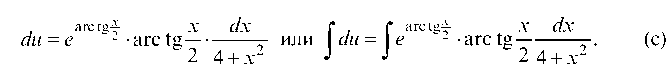
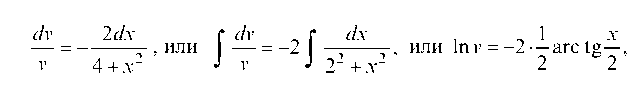
Чтобы взять интеграл в правой части, введем новую переменную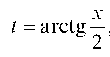 , тогда
, тогда
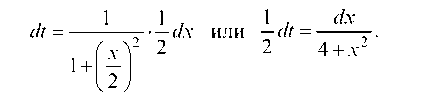
Выражение (с) примет вид

Этот интеграл берется по частям по формуле но функции и (x) и v(x) здесь совсем другие, чем (b) и (с).
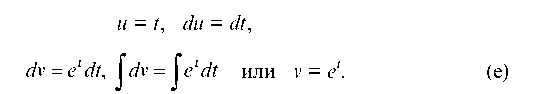
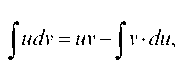
С использованием выражений (е) интеграл (d) с использованием формулы интегрирования по частям запишется как

Подставляя сюда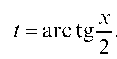 , получим:
, получим:
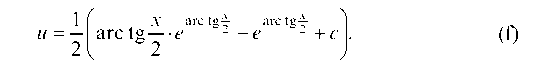
Следовательно, решение исходного дифференциального уравнения имеет вид:
Это, так называемое, дифференциальное уравнение Бернулли вида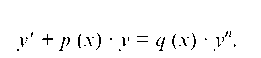
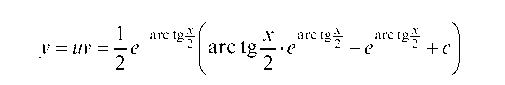
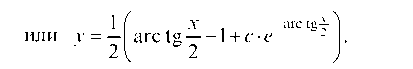

Сначала его нужно разделить на yn, а затем ввести вспомогательную функцию z = y - n + 1.
Делим исходное уравнение на у2
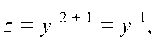
Пусть найдем
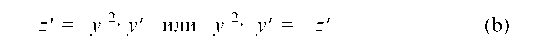
Подставляем функции (b) в уравнение (а)

Получили линейное дифференциальное уравнение, которое решаем методом Бернулли

Подставляем функции (d) в уравнение (с)

и группируем
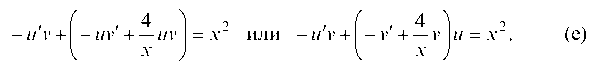
Пусть

Отсюда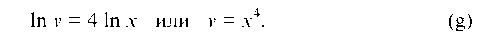
Подставляем (g) в уравнение (е) или при х ф 0
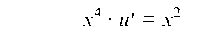
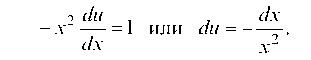
Интегрируем
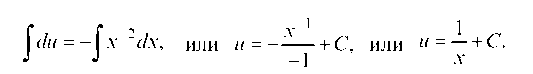
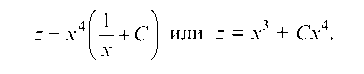
Из выражения (b)

Таким образом, решение исходного дифференциального уравнения имеет вид:
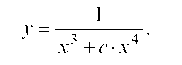
8.1.2. Скорость роста банковского вклада пропорциональна с коэффициентом равным m = 3 величине вклада. Найти закон изменения величины вклада со временем, если первоначальная сумма вклада составляла n = 2 миллионов рублей.
Если величину вклада обозначить через J = J (t), где t - время,
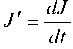
то скорость роста вклада есть производная, т. е. и она про
порциональна величине вклада J с коэффициентом пропорциональности, равным 3, т. е.
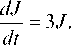
В начальный момент времени, т. е. при t = 0 начальный вклад J0 = 2 млн руб. Тогда
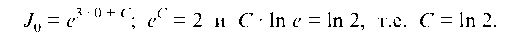
Разделяем переменные и интегрируем
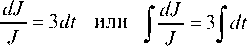

Окончательно: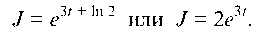
8.2.1. Решить задачу Коши:
а) у'" - 2у " - 3у' = 0, у (0) = 0, у' (0) = 3, у " (0) = 1.
Понизим порядок дифуравнения, обозначив t = у', тогда t' = у ", t" = у'" и уравнение имеет вид:
2
Его характеристическое уравнение r - 2r - 3 = 0, корни которого r1 = -1, r2 = 3. Тогда решение уравнения (а) имеет вид:
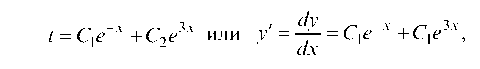
отсюдаИнтегрируя это выражение, по
лучим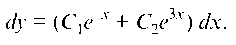
Это есть общее решение исходного дифференциального уравнения.
Используя начальные условия, найдем постоянные С\, С2, С3: 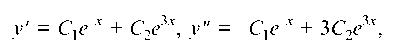 тогда
тогда
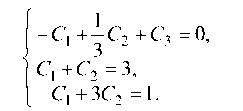
Из этой системы <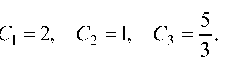
А частное решение исходного однородного дифференциального уравнения с постоянными коэффициентами, удовлетворяющее начальным условиям, будет:


Находим общее решение однородного дифференциального уравнения (дифура), соответствующего исходному дифуру (а):

Его характеристическое уравнение r - 6r + 9 = 0, а корни r1 = r2 = 3. Тогда общее решение дифура (b) будет:

Частное решение исходного дифура (а) берем в виде:

тогда
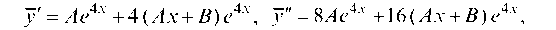
подставляем в (а) и группируем: (2A + B) + Ax = 1 + x, отсюда, приравняв коэффициенты при одинаковых степенях х, имеем:
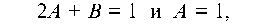
т. е. A = 1, B = -1, а выражение (d) принимает вид:

Суммируя (с) и (е), найдем общее решение неоднородного дифференциального уравнения (а):

Найдем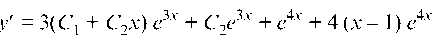 И исполь
И исполь
зуя начальные условия (а), имеем:
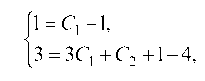
отсюда C1 = 2, C3 = 0.
Найденные значения C и C2 подставляем в (f) и частное решение исходного дифференциального уравнения имеет вид:
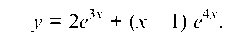
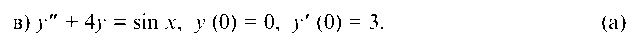
Однородное дифуравнение

имеет характеристическое уравнение r2 + 4 = 0, a его корни будут r12 = ± 2i Тогда общее решение дифура (b) будет:
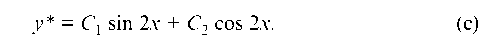
Частное решение дифура (а) ищем в виде:

Определив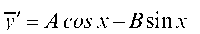 И
И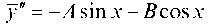 И под
И под
ставив в (а), после группировки имеем
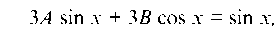
отсюда 3А = 1, 3B = 0 или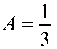 И B = 0. Подставляя А и B в (d)
И B = 0. Подставляя А и B в (d)
и суммируя с (с), найдем общее решение дифура (а):
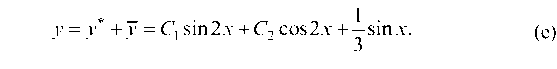
Найдем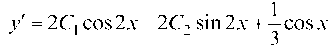 И, используя на
И, используя на
чальные условия (а), имеем
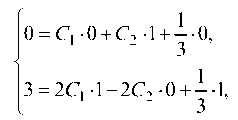
отсюда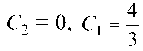 .
.
Подставляя найденные С и С2 в (е), будем иметь решение исходного дифференциального уравнения (а), удовлетворяющего начальным условиям: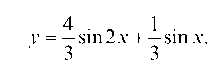
3.3.1. Решить систему линейных уравнений
- = 2 x - 4 у, dt
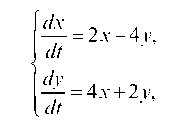
^ = 4 x+2 у,
dt у'
с начальными условиями х (0) = 1, у(0) = 2.
Продифференцируем первое уравнение системы
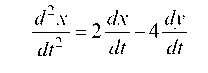
d2 x „ dx. йу
—- = 2--4 —
dt2 dt dt
и подставим в него у' из 2-го уравнения системы
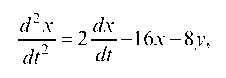
d2 x „ dx, ^
—— = 2--16x - 8у,
dt2 dt
а в это уравнение подставим у из 1-го уравнения системы, имеем: d2 x dx
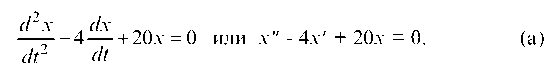
—--4 — + 20x = 0 или х" - 4х'+ 20х = 0. (а)
dt2 dt V '
Его характеристическое уравнение r - 4r + 20 = 0, корни которого r = 2 ± 4г. Тогда дифференциальное уравнение (а) имеет решение:
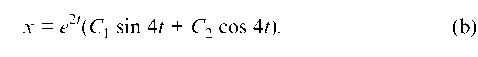
Подставляя это решение в 1-ое уравнение системы, после группирования найдем, что
x = e2t(C1 sin 4t + C2 cos 4t). (b)
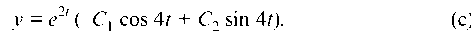
Подставляя в (b) и (с) начальные условия, определим, что
у = e2t (-С1 cos 4t + С2 sin 4t). (c)
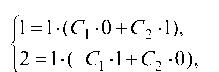
1 = 1-(C1 • 0 + C2-1),
2 = 1-(-C1 -1 + C2 -0),
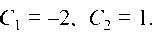
отсюда C1 = -2, C2 = 1. 252
Подставив эти константы в (b) и (с), найдем решение исходной системы дифференциальных уравнений
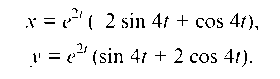
9. РЯДЫ
9.1.1. Исследовать на сходимость ряды с положительными членами:
Применим необходимый признак сходимости числового ряда. Если lim ak = 0, то ряд возможно сходится, если lim ak ф 0, то
ряд расходится.
Для нашего примера:
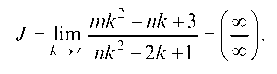
Имеем неопределенность, числитель и знаменатель делим на k2
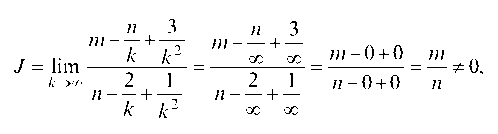
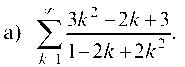
Рассмотрим общий член
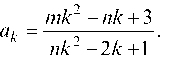
так как по условию m ф 0.
Следовательно, у всех студентов ряд расходится, так как не выполняется необходимый признак сходимости числового ряда.
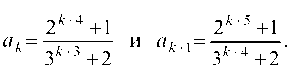
Исследуем сходимость ряда по признаку Даламбера:
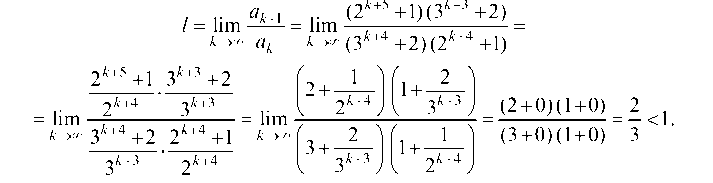
Следовательно, ряд сходится.
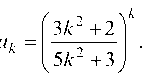
По признаку Коши имеем:
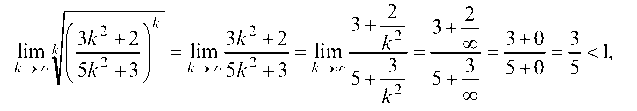
следовательно, ряд сходится. Пример сконструирован так, что коэффициент (m + п) перед к2 в знаменателе больше, чем коэффициент m перед k2 в числителе, а поэтому всегда предел будет меньше единицы, т. е. ряд будет сходящийся.
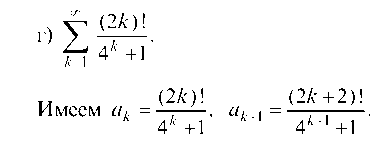
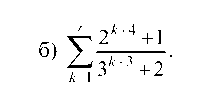
Имеем
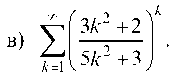
Имеем
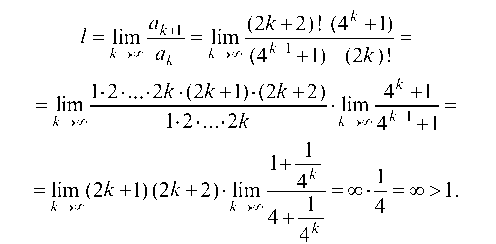
Следовательно, ряд расходится
9.2.1. Найти область сходимости степенного ряда:
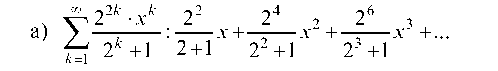
Согласно признаку Даламбера искомый ряд сходится при тех значениях х, для которых:

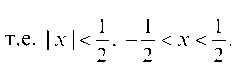
Исследуем сходимость ряда на концах интервала. При x = - 2 получаем числовой ряд
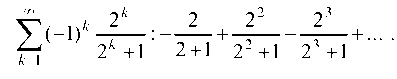
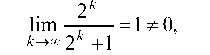
т. е. по признаку Лейбница ряд расходится.
При Имеем числовой ряд с положительными членами
Имеем числовой ряд с положительными членами
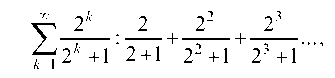
который расходится, так как предел общего числа не равен нулю. Итак, область сходимости данного ряда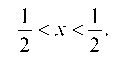
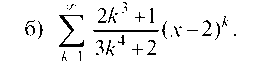
Применим признак Даламбера:
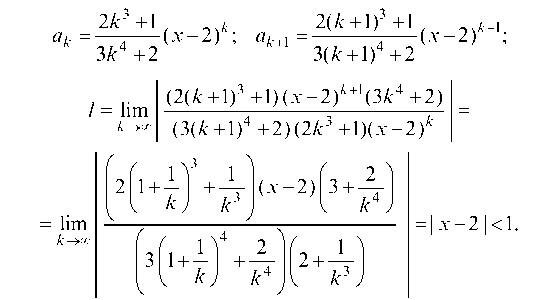
Отсюда заключаем, что ряд сходится при -1 < x - 2 < 1, или 1 < x < 3.
При х = 1 получаем знакочередующийся ряд
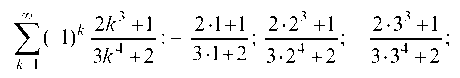
который сходится по признаку Лейбница, так как его члены убывают, а предел общего члена при k ® да равен нулю.
который расходится.
Воспользуемся предельным признаком сравнения. Так как предел
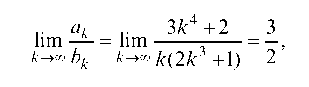
лежит между 0 и да, то оба ряда расходятся, т. е. при х = 3 исходный ряд расходится.
Итак, область сходимости данного ряда: 1 < х < 3.
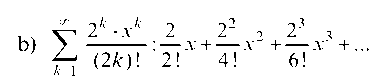
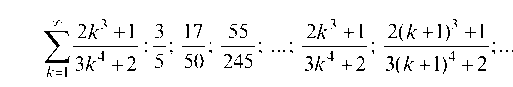
Сравним его с гармоническим рядом
Применим признак Даламбера:
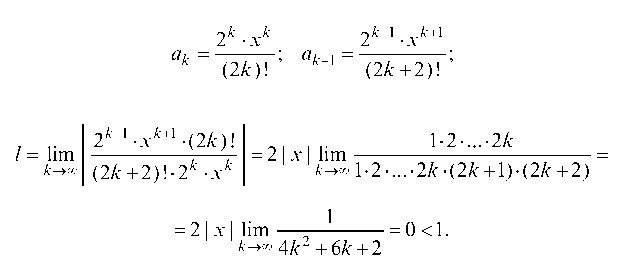
Следовательно, при любом конечном х по признаку Даламбе-ра данный ряд абсолютно сходится. Область сходимости рассматриваемого ряда есть вся числовая ось.
9.2.2. Разложить функцию f (х) в ряд Тейлора в окрестности точки х0:
а) У(х) = —+-’ Хо = 3. х + 4
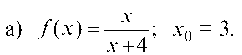
Запишем функцию в виде:
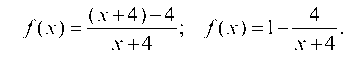
) (х + 4) - 4 1 4
f (х) =-1— ’ f (х) =1 -
Вычислим значения данной функции и ее последовательных производных при х0 = 3:
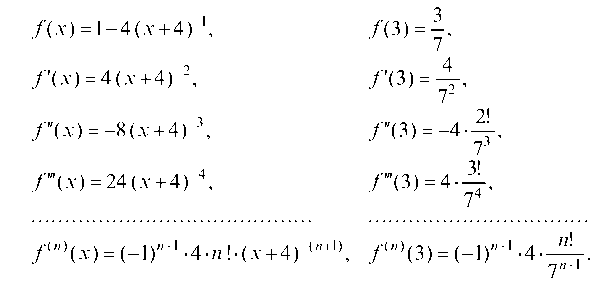
Подставляя полученные значения в общее выражение ряда Тейлора для произвольной функции f(x) = /(х0) + f'(x0)(x - х0) +
+ ЛМ (х - х0)2 + (х - х-0)3 + ... + ^ (х - х0)П....
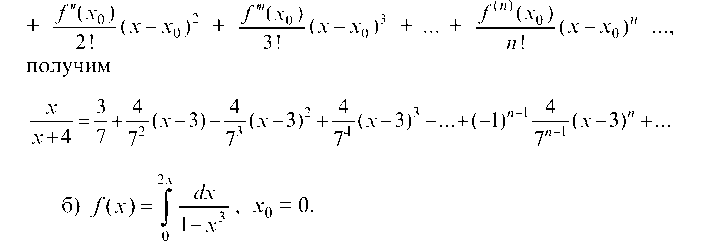
- I!
б) /(х) = [-^г, Х0 = 0.
Возьмем табличное разложение
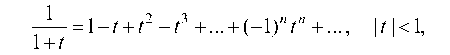
3
в котором положим г = - х. 258

Интегрируем этот ряд:
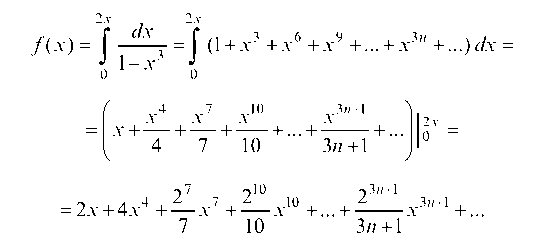
Имеем
/(х) = ( -= ( (1 + х3 + х6 + х9 +... + х3и + ...) Іх =
гу7 л10 г\ 3п+1
= 2х + 4 х4 + — х7 +-х10 +... +-х 3п+1 +...
Получили искомое разложение.
9.2.3. С помощью разложения в ряд вычислить приближенно с точностью 0,001 значения:
Берем разложение функции / (х) = ех в ряд Тейлора:
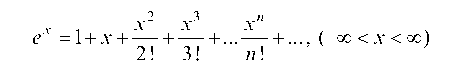
х2 х3 хп
ех = 1 + х +-+-+ ...-+ ... , (-¥< х <¥)
2 ! 3 ! п!
и подставляем в него х = -3:
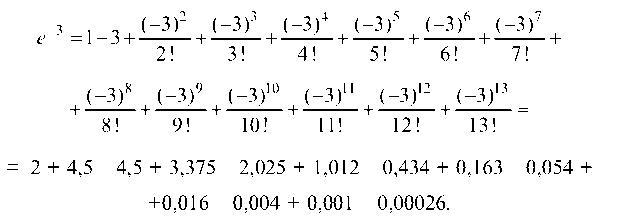
е-3 = 1 - 3+(-32+(-33+(-324+(-31+(-36+(-37+
2 ! 3 ! 4 ! 5 ! 6 ! 7 !
+ (-В/ + (-3)9 + (-3Т + (-3Ц + НОИ + (-3)13 =
і! 9 ! 10! 11! 12! 13 !
=-2 + 4,5 - 4,5 + 3,375 - 2,025 + 1,012 - 0,434 + 0,163 - 0,054 + +0,016 - 0,004 + 0,001 - 0,00026.
Полученный ряд знакочередующийся. Поэтому, ограничиваясь первыми двенадцатью членами ряда, мы получим ошибку
0,00026 < 0,001.
_3
и подставим в него t = x2:

Рассмотрим функцию:
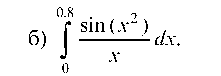
Возьмем табличное разложение:
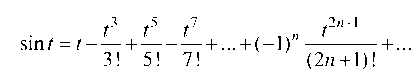
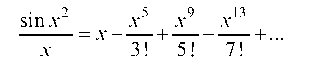
и проинтегрируем ее:
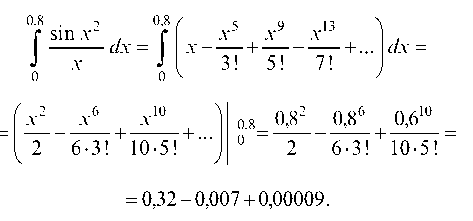
Ограничиваясь первыми двумя членами ряда (ошибка при этом не превосходит 0,00009 < 0,001) имеем окончательно:
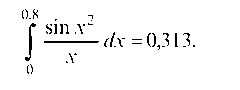
| < Предыдущая | Следующая > |
|---|