Решение типовых задач контрольной работы по специальным разделам высшей математики
6. ДВОЙНЫЕ, ТРОЙНЫЕ И КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ
6.1.1. Изменить порядок интегрирования:
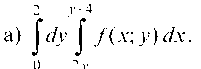
2 у+4
а) /у { /(х; у) йх.
0 2 у
Область интегрирования (заштрихована) (рис. 57) ограничена снизу и сверху прямыми у = 0 и у = 2, а слева и справа прямыми х = 2у и х = у + 4. Меняем пределы интегрирования, тогда в направлении оси 0у на х е [0; 6] нужно выделить две области: х е [0; 4] и х е [4; 6] и первая область Д1 будет ограничена снизу
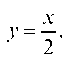
х
и сверху прямыми: у = 0 и у — —, а вторая область — у = х - 4 и у = 2. 2
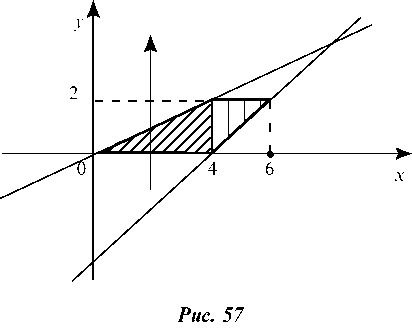
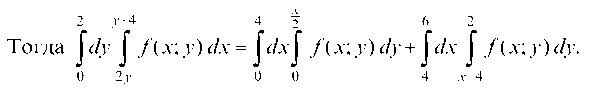
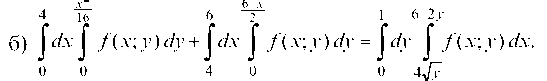
Строим область интегрирования D (рис. 58). Она состоит из двух областей: D1 - на отрезке х е [0; 4] ограниченной снизу и
сверху кривыми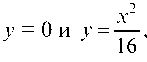 И D2 — на отрезке х е [4; 6] огра
И D2 — на отрезке х е [4; 6] огра
ниченной снизу и сверху прямыми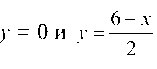 .
.
y
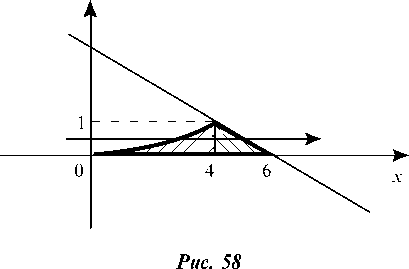
При изменении порядка интегрирования будем иметь правильную область D, ограниченную слева и справа кривыми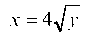
и х = 6 - 2у, а снизу и сверху прямыми y = 0 и y = 1. Ответ записан наверху.
6.1.2. Найти объем тела, ограниченного поверхностями: z = 0; y = x2 и плоскостью, проходящей через точки A (2; 4; 0), B (-4; 4; 0), C (0; 0; 6).
Составим уравнение плоскости, проходящей через три заданные точки:
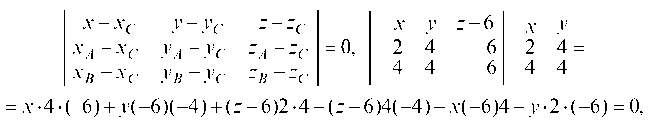
или
или
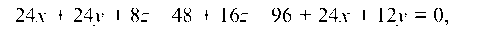
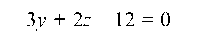
и окончательно
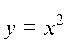
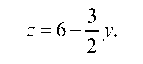
2
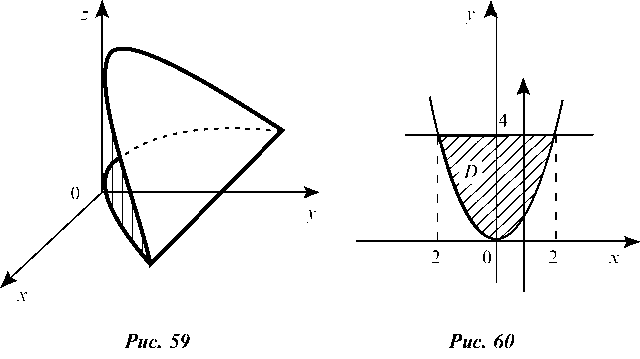
Изобразим тело (рис. 59): параболический цилиндр у = х ог-
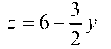
3
раничен снизу плоскостью г = 0, а сверху — плоскостью г = 6 - 7 у
параллельной оси Ох. Область интегрирования Б (рис. 60) есть фигура ограниченная параболой у = х и прямой у = 4.
В силу симметрии тела относительно плоскости гОу удвоим интеграл:
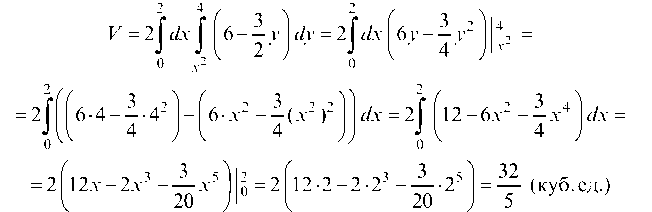
6.1.3. Изобразить и найти площадь фигур, ограниченных линиями:
а) у = 0; у = х2 и у = 4 (х - 6)2.
Построим две параболы и найдем их точки пересечения:
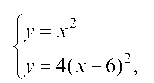
отсюда х2 = 4(х - 6)2 или х2 - 16х + 48 = 0, его корни х1 = 4 и х2 = 12. На чертеже (рис. 61) изображена заштрихованная фигура, площадь которой определяем:
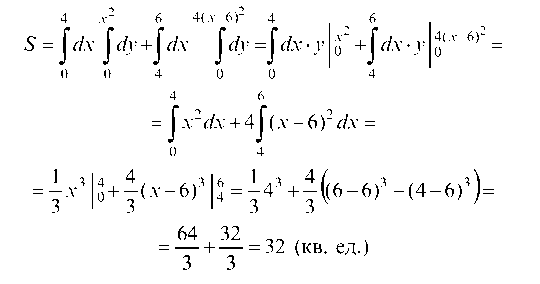
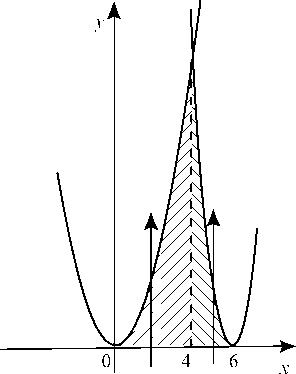
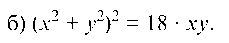
б) (x2 + у2)2 = 18 ¦ xy.
В полярных координатах это уравнение запишется в виде (смотрите пример 4.4.16): р = 9 sin 2p. Рассмотрим заштрихованную область, для нее координаты р и p определены неравенствами 0 <р<Р, 0 <р< Зд/ sin 2р.
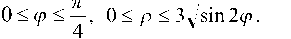
Тогда
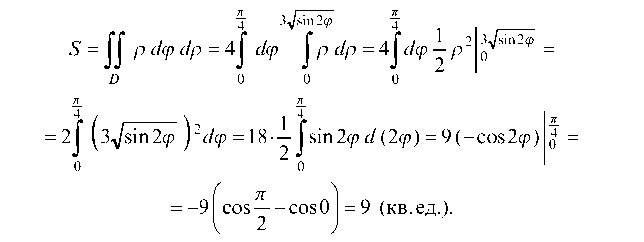
| < Предыдущая |
|---|