Программа курса математики
Раздел I. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ, ВЕКТОРНАЯ АЛГЕБРА, ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ
Аналитическая геометрия на плоскости
1. Прямоугольные и полярные координаты на плоскости; основные задачи. Преобразования координат.
2. Уравнение линии на плоскости. Параметрические уравнения линии; уравнения в полярных координатах. Примеры.
3. Уравнения прямой, основные задачи.
4. Канонические уравнения кривых второго порядка; их основные свойства.
Определители и системы линейных уравнений
5. Определители второго и третьего порядков. Решение систем линейных уравнений с двумя и тремя неизвестными.
6. Векторы на плоскости и в пространстве. Сложение и вычитание векторов. Умножение вектора на скаляр. Проекции вектора на ось. Система декартовых прямоугольных координат в пространстве. Проекции вектора на оси координат. Направляющие косинусы вектора. Длина и координаты вектора. Действия над векторами, заданными своими координатами.
7. Скалярное произведение двух векторов и его свойства; векторное произведение; смешанное произведение трех векторов.
Аналитическая геометрия в пространстве
8. Прямоугольные координаты; основные задачи.
9. Уравнение поверхности. Цилиндрические поверхности. Уравнения пространственных линий.
10. Уравнение плоскости и уравнения прямой в пространстве; основные задачи.
11. Канонические уравнения поверхностей второго порядка.
12. Решение систем линейных уравнений методом Гаусса.
13. Определители n-го порядка и их свойства. Решение систем по формулам Крамера.
14. Матрицы. Сложение матриц; умножение матрицы на число; произведение матриц. Единичная матрица. Обратная матрица.
15. Собственные числа и собственные векторы квадратной матрицы.
16. Векторное пространство. Линейная зависимость и независимость систем векторов. Базис векторного пространства.
17. Линейное преобразование. Матрица линейного преобразования.
18. Теорема Кронеккера — Капелли и ее приложение к исследованию и решению системы линейных уравнений.
19. Квадратичные формы; положительно определенные квадратичные формы. Приведение квадратичной формы к диагональному виду. Применение матриц к упрощению уравнений кривых второго порядка на плоскости.
РАЗДЕЛ II. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ Функции, предел, непрерывность
20. Переменные и постоянные величины. Функции; область определения; способы задания. График функции и его построение; преобразование графиков. Основные элементарные функции.
21. Предел; основные свойства пределов. Бесконечно малые и бесконечно большие. Формулировка теоремы существования предела для монотонной последовательности и монотонной функции.
22. Пределы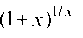и
При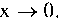
Число е; натуральные логарифмы.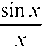
23. Сравнение бесконечно малых; эквивалентные бесконечно малые.
24. Непрерывность функции в точке и на интервале; действия над непрерывными функциями. Формулировка основных свойств функций, непрерывных на замкнутом интервале. Точки разрыва функции.
25. Задачи, приводящие к понятию производной. Определение производной; ее геометрический и механический смысл; уравнение касательной к графику функции.
26. Основные правила нахождения производных.
27. Дифференциал функции; его геометрический смысл. Линеаризация функции. Дифференциал сложной функции.
28. Производные высших порядков.
29. Функции, заданные параметрически; их дифференцирование.
30. Теоремы Ролля и Лагранжа.
31. Правило Лопиталя.
32. Формула Тейлора.
33. Возрастание и убывание функций; необходимые и достаточные условия.
34. Экстремум функции. Необходимое условие, достаточные условия. Наибольшее и наименьшее значения функции на замкнутом интервале.
35. Выпуклость и вогнутость графика функции; точки перегиба.
36. Асимптоты графиков функций: вертикальные, горизонтальные и наклонные.
37. Функции двух и трех переменных как функции точки. Геометрическое изображение функции двух переменных с помощью поверхностей и линий уровня.
38. Предел функций точки. Непрерывность в точке и в области. Частные производные от функции нескольких переменных; геометрический смысл частных производных функций двух переменных.
39. Производная по направлению и градиент функции; основные свойства градиента.
40. Полный дифференциал функции нескольких переменных; достаточные условия его существования. Понятие о частных производных высших порядков.
41. Экстремум функции нескольких переменных. Необходимые условия экстремума. Наибольшее и наименьшее значения функции в ограниченной замкнутой области.
42. Условный экстремум; необходимое условие. Метод множителей Лагранжа.
43. Первообразная функция и неопределенный интеграл. Основные свойства неопределенного интеграла. Таблица основных интегралов.
44. Непосредственное интегрирование. Интегрирование заменой переменного. Интегрирование по частям. Простейшие типы интегралов. Использование таблиц неопределенных интегралов.
45. Задачи, приводящие к понятию определенного интеграла. Определенный интеграл от непрерывной функции как предел интегральной суммы; формулировка теоремы о его существовании. Основные свойства определенного интеграла; теорема о среднем. Среднее значение функции.
46. Производная от определенного интеграла по верхнему пределу. Формула Ньютона — Лейбница. Связь между определенным и неопределенным интегралами.
47. Методы вычисления определенного интеграла; интегрирование заменой переменного и интегрирование по частям.
48. Несобственные интегралы с бесконечными пределами.
Приложения определенного интеграла
49. Вычисление площадей в декартовых координатах. Определение и вычисление объема тела по площадям параллельных сечений; объем тела вращения.
50. Определение и вычисление длины дуги плоской кривой.
51. Задачи геометрического и физического характера, приводящие к понятию двойного интеграла. Двойной интеграл; формулировка теоремы о его существовании.
52. Выражение двойного интеграла в декартовых и полярных координатах через повторный интеграл.
53. Применение двойных интегралов к геометрическим и физическим задачам. Вычисление интеграла Пуассона
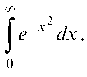
Общие понятия. Дифференциальные уравнения первого порядка
54. Задачи геометрического и физического характера, приводящие к дифференциальным уравнениям. Дифференциальные уравнения первого порядка. Задача Коши; частное и общее решения.
55. Дифференциальные уравнения с разделяющимися переменными. Однородные и линейные уравнения первого порядка.
Дифференциальные уравнения второго порядка
56. Интегрирование некоторых уравнений второго порядка путем понижения порядка уравнения.
57. Общие сведения о линейных дифференциальных уравнениях второго порядка. Структура общего решения.
58. Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами. Характеристическое уравнение. Общее решение линейного однородного дифференциального уравнения с постоянными коэффициентами. Отыскание частного решения неоднородного линейного уравнения методом неопределенных коэффициентов.
59. Числовые ряды. Сходимость и расходимость. Необходимые условия сходимости; основные свойства.
60. Достаточные признаки сходимости и расходимости рядов с положительными членами. Признак Даламбера. Оценка остатка ряда.
61. Признак Лейбница о сходимости знакопеременных рядов; оценка остатка ряда.
62. Абсолютная и неабсолютная сходимости рядов. Свойства абсолютно сходящихся рядов.
63. Функциональный ряд; область его сходимости. Степенной ряд. Теорема Абеля. Интервал сходимости; радиус сходимости.
64. Разложение функции в степенной ряд. Достаточные условия разложимости функции в ряд Тейлора. Разложение в ряд Тейлора (Маклорена) функций: ех, cos x, sin x, ln(1 + x), (1 + x)m.
65. Интегрирование и дифференцирование степенных рядов.
В учебном пособии будут также приведены некоторые специальные разделы «Высшей математики».
Раздел VI. ТЕОРИЯ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
66. Случайные события. События и вероятность. Алгебра событий. Классическое и статистическое определение вероятности. Условная вероятность. Зависимые и независимые события. Теоремы сложения и умножения вероятностей. Формула полной вероятности.
67. Случайные величины. Закон распределения дискретной случайной величины. Биномиальное распределение. Распределение Пуассона. Простейший поток событий. Числовые характеристики. Числовые характеристики дискретных и непрерывных случайных величин. Показательное распределение. Нормальное распределение. Закон больших чисел.
68. Математическая теория выборки. Сплошное и выборочное наблюдения. Статистические оценки. Требования, предъявляемые к статистическим оценкам. Методы построения статистических оценок. Оценка доли признака. Точечные оценки для средней и дисперсии генеральной совокупности. Интервальные оценки средней и дисперсии нормально распределенной генеральной совокупности.
69. Статистическая проверка гипотез. Критерий проверки. Критическая область. Общая схема проверки гипотезы. Проверка гипотез относительно средней. Сравнение дисперсий двух совокупностей. Сравнение двух зависимых выборок. Критерий согласия.
70. Элементы теории корреляции. Основные понятия. Отыскание параметров выборочного уравнения прямой линии регрессии по несгруппированным и по сгруппированным данным. Коэффициент корреляции и его свойства.
Раздел VII. МАТЕМАТИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
71. Математические методы в экономике. Экономические примеры. Общая задача линейного программирования (с ограничениями в форме уравнений и неравенств). Понятие плана, оптимального плана.
72. Основная задача линейного программирования (с ограничениями в форме уравнений) и ее геометрическая интерпретация. Выпуклость множества планов. Понятие опорного плана (базисного решения). Экстремальная точка в множестве планов.
73. Достаточные условия существования оптимального опорного плана (теорема существования).
Базисный план. Метод последовательного улучшения базисного плана (симплекс-метод). Некоторые варианты симплекс-метода
74. Двойственные задачи. Соотношения между значениями целевых функций двойственных задач (основное неравенство двойственности). Теоремы двойственности и критерии оптимальности планов двойственных задач.
Экономическая интерпретация двойственных задач. Критерий Канторовича оптимальности плана задачи использования ресурсов.
75. Простейшие линейные задачи экономики: основная задача текущего производственного планирования; задача о комплексном выпуске продукции; задача о распределении программы и специальный метод ее решений (метод разрешающих множителей).
76. Транспортная задача в матричной и сетевой постановке. Метод потенциалов.
77. Понятие о распределительной задаче.
78. Целочисленное линейное программирование.
79. Элементы теории матричных игр.
80. Понятие о графах и сетевом планировании.
81. Понятие о выпуклом программировании.
82. Вычислительные методы квадратичного программирования.
83. Простейшие задачи динамического программирования.
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ. ВЕКТОРНАЯ АЛГЕБРА. ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ
| < Предыдущая | Следующая > |
|---|
