6.4.4. Выборочная дисперсия

Пусть значения Св X образуют генеральную совокупность. Дисперсию В (X) Св X будем называть генеральной дисперсией и

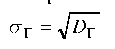
обозначать Вг, а среднее квадратическое отклонение стг = л/В7 Требуется найти статистическую оценку для Вг.

Пусть _1, _2, ., _п — выборка из генеральной совокупности X, а XI, X2, ..., Xn - п экземпляров X. Рассмотрим статистическую оценку

1 п

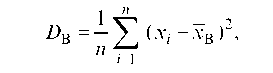
которая называется выборочной дисперсией. Вв — случайная величина. Ее конкретное значение при данной выборке _1, ..., _п

329

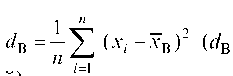
персией).

Если выборка из генеральной совокупности задана в виде таблицы

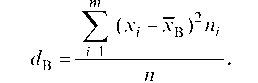
Тогда

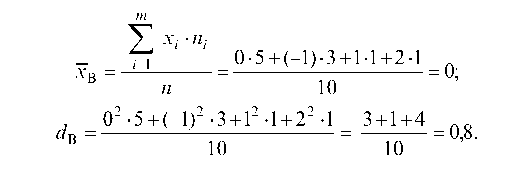
Пример 6.33. Пусть выборка задана таблицей

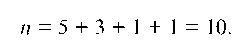
DB является смещенной статистической оценкой для D (X). Поэтому рассматривают статистическую оценку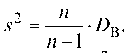, ко

торая называется исправленной выборочной дисперсией. s2 является несмещенной статистической оценкой для Dr Нетрудно видеть, что при больших n: s2 » DB.

Величина называется выборочным среднеквадрати

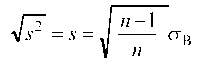
ческим отклонением, а — исправленным вы

борочным среднеквадратическим отклонением.

Пример 6.34. Пусть генеральная совокупность X подчинена нормальному закону. Требуется оценить ее параметры.

Так как параметрами нормального распределения являются s = стг и a = M (X) = хг, то

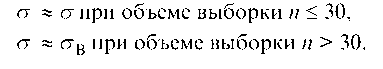
< Предыдущая		Следующая >