6.4.3. Генеральная средняя. Выборочная средняя
Пусть значения случайной величины X образуют генеральную совокупность. Математическое ожидание X будем называть генеральной средней и обозначать хг т. е. хг = М (X).
Рассмотрим некоторую выборку хь х2, ..., хп (варианты могут повторяться) из генеральной совокупности X. Будем ее рассматривать как значения п экземпляров X!, Х2, ..., Хп СВ X. Рассмотрим статистическую оценку
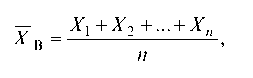
которая называется выборочной средней. Конкретное значение статистической оценки X в при выборке _1, _2, ..., _п будет:
_ _ + х2 +... + _и _ В _
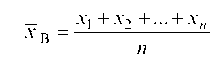
п
(статистическая оценка X в является СВ, а _ в — конкретное значение X в, зависящее от выборки).
В дальнейшем и _ в будем называть выборочной средней. Если выборка задана в виде таблицы

2 _ ' п1 .=1_
п
то ясно, что п = п1 + п2 + . + пт
_1 • п1 + _2 • п2 +... + _т • пт
т
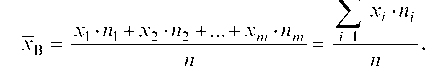
выборочная средняя X в является эффективной, несмещенной и состоятельной статистической оценкой для математического
ожидания М(X), т. е. для генеральной средней X г.
| < Предыдущая | Следующая > |
|---|