6.4.5. Интервальные оценки параметров распределения. Доверительный интервал для математического ожидания нормального распределения при известном s
Пусть CB X образуют генеральную совокупность и в — неизвестный параметр CB X. Если статистическая оценка в * является состоятельной, то чем больше объем выборки, тем точнее получаем значение в. Однако на практике мы имеем выборки не очень большого объема, поэтому не можем гарантировать большую точность.
Пусть в* — статистическая оценка для в. Величина |в* - в| называется точностью оценки. Ясно, что точность является CB, т. к. в* — случайная величина. Зададим малое положительное число 8 и потребуем, чтобы точность оценки |в* - в| была меньше 8, т. е. | в* - в | < 8.
Мы не можем категорически утверждать, что оценка в * удовлетворяет неравенству | в* - в | < 8; можно лишь говорить о вероятности g, с которой это неравенство выполнится.
Надежностью g или доверительной вероятностью оценки в по в * называется вероятность g, с которой осуществляется неравенство |в * - в| < 8, т. е.
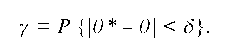
Обычно надежность g задают наперед, причем, за g берут число, близкое к 1 (0,9; 0,95; 0,99; ...).
Так как неравенство |в * - в| < S равносильно двойному неравенству в* - S < в < в* + 8, то получаем:
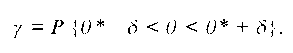
Интервал (в * - 8, в* + 5) называется доверительным интервалом, т. е. доверительный интервал покрывает неизвестный параметр в с вероятностью у. Заметим, что концы доверительного интервала являются случайными и изменяются от выборки к выборке, поэтому точнее говорить, что интервал (в * - 8, в * + 8) покрывает неизвестный параметр в, а не в принадлежит этому интервалу.
Пусть генеральная совокупность задана случайной величиной X, распределенной по нормальному закону, причем, среднее квадратическое отклонение а известно. Неизвестным является математическое ожидание а = М (X). Требуется найти доверительный интервал для а при заданной надежности у.
Выборочная средняя
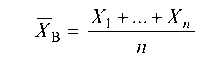
является статистической оценкой для хг = а.
Теорема. Случайная величина хВ имеет нормальное распределение, если X имеет нормальное распределение, и М (ХВ) = а,
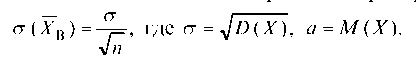
А (XВ) = а, где а = у/Б (X), а = М (X). л/и
Доверительный интервал для а имеет вид:
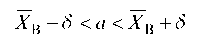
и
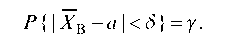
Находим 8.
Пользуясь соотношением

где Ф(г) — функция Лапласа, имеем:
Р { | XВ - а | <8} = 2Ф
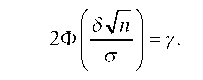
таблице значений функции Лапласа находим значение t.
Обозначив
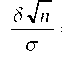
= t, получим F(t) = g Так как g задана, то по
Из равенства Находим
Находим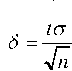 — точность оценки.
— точность оценки.
Значит, доверительный интервал для а имеет вид:
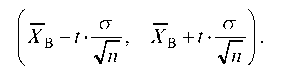
Если задана выборка из генеральной совокупности X
| нГ | к" | X2 | Xm |
| n. | n1 | n2 | nm |
n = U1 + ... + nm, то доверительный интервал будет:
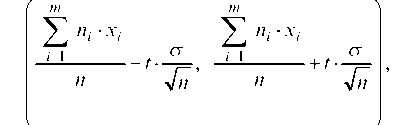
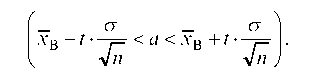
т. е.
Пример 6.35. Найти доверительный интервал для оценки математического ожидания а нормального распределения с надежностью 0,95, зная выборочную среднюю Xb = 10,43, объем выборки n = 100 и среднее квадратическое отклонение s = 5.
Решение. Воспользуемся формулой

Найдем t. Из соотношения 2Ф (t) = 0,95 получим: Ф (t) = 0,475. По таблице находим t = 1,96. Найдем точность оценки 
Искомый доверительный интервал (10,43 - 0,98 < a < 10,43 + 0,98) или (9,45 < a < 11,41).
Смысл полученного результата таков: если будет произведено большое число выборок, то 95% из них определят такие доверительные интервалы, в которых математическое ожидание будет заключено.
| < Предыдущая | Следующая > |
|---|