6.5. Методы расчета характеристик выборки. 6.5.1. Условные варианты. Метод произведений
Рассмотрим рациональные методы определения характеристик выборки Xb и dB.
6.5.1. Условные варианты.
Метод произведений
Пусть выборка из генеральной совокупности X является вариационным рядом с равноотстоящими вариантами, т. е.
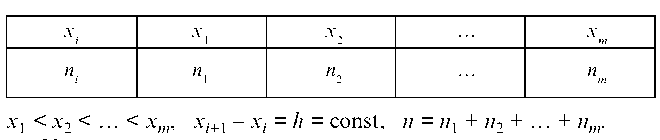
Условными называют варианты Ui, определяемые равенством
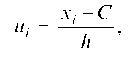
где С — ложный нуль. Обычно полагают С равным варианте с наибольшей частотой.
Нетрудно видеть, что условные варианты принимают только целые значения, и, если xi0 = C, то Ui0 = 0.
Условные варианты U1, U2, ..., Un образуют условную выборку

Тогда можно определить условные эмпирические моменты порядка ;:
т

м; = -.
п
Определив условные выборочные моменты первого и второго порядка

тт
2 П • мг' 2 П ¦ м* = -; м2* = -,
пп можно определить выборочные среднюю и дисперсию: хв = М* • к + С; 4 = [м2* -(м*)2]• А2.
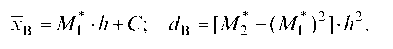
Пример 6.36. Даны выборочные варианты х. и соответствующие частоты пг - количественного признака X:

Найти методом произведений выборочные среднюю, дисперсию и среднее квадратическое отклонение.
Решение. Составим расчетную таблицу, для чего:
1) запишем варианты х. в первый столбец;
2) запишем частоты пг - во второй столбец;
3) в качестве ложного нуля С выберем варианту 20 (эта варианта имеет наибольшую частоту); в клетке третьего столбца, которая принадлежит строке, содержащей варианту 20, пишем 0; над нулем последовательно записываем условные варианты -1, -2, а под нулем — последовательно 1, 2;
4) произведения частот на условные варианты мг - записываем в четвертый столбец; находим сумму этих произведений и помещаем ее в нижнюю клетку столбца;
5) произведения частот на квадраты условных вариант запишем в пятый столбец; сумму чисел столбца (80) помещаем в нижнюю клетку столбца;
6) произведения частот на квадраты условных вариант, увеличенных на единицу, запишем в шестой (контрольный) столбец; сумму чисел столбца (188) помещаем в нижнюю клетку столбца. В итоге получим следующую расчетную таблицу:
| x. | n. | u. | n. ¦ u. | ni •u.2 | n. (u. + 1)2 |
| 10 | 6 | -2 | -12 | 24 | 6 |
| 15 | 16 | -1 | -16 | 16 | 0 |
| 20 | 50 | 0 | 0 | 0 | 50 |
| 25 | 24 | 1 | 24 | 24 | 96 |
| 30 | 4 | 2 | 8 | 16 | 36 |
| n = 100 | £ n u. = 4 | £ n. u2 = 80 | £ n. (u. +1)2 = 188 |
Контроль
£ ni • u2 +2 £ n. • u. + n = 80 + 2 • 4 +100 = 188;
£ n. (и. +1)2 = 188.
Совпадение найденных сумм свидетельствует о том, что вычисления произведены правильно.
Вычислим условные моменты первого и второго порядков:
| < Предыдущая | Следующая > |
|---|