6.5.2. Эмпирические и теоретические частоты
Пусть значения СВ X образуют генеральную совокупность. Закон распределения X неизвестен.
Рассмотрим некоторую выборку объема п из генеральной совокупности

п = + ... + пт.
Частоты п; появления вариант х; также называют эмпирическими частотами.
Пусть X — дискретная СВ и имеются основания предположить, что изучаемая величина X распределена по некоторому определенному закону. Зная закон распределения X, мы можем найти вероятности р появления значений х;, т. е.
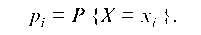
Р = р }•
Теоретическими частотами п; называют частоты, определяемые по формуле п, = п • р.
Нетрудно видеть, что п; указывает, сколько раз должно появиться в среднем значение х; случайной величины X с предполагаемым законом распределения.
Пусть теперь X — непрерывная СВ. Рассмотрим более детально определение теоретических частот, предполагая, что X — нормально распределенная случайная величина.
Пусть

п = п1 + ... + пт, равноотстоящая выборка из генеральной совокупности X, п1 , ... , пт — эмпирические частоты, хг-+1 - хг - = А. Тогда теоретические частоты определяются по формуле

где р — вероятность попадания X в ;-ый частичный интервал с
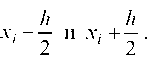
к к концами х; — и X; + — .
; 2 ; 2

Значения функции j (u) находятся по таблице.
| < Предыдущая | Следующая > |
|---|