6.3.4. Непрерывные распределения

6.3.4.1. Равномерное распределение

Распределение вероятностей называется равномерным, если дифференциальная функция имеет постоянное значение на интервале, которому принадлежат все возможные значения случайной величины, т. е. f (x) = C на (a; b) и f (x) = 0 при всех остальных значениях х.

Из условия

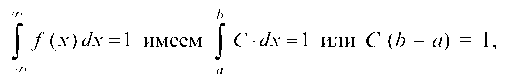
отсюда

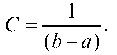
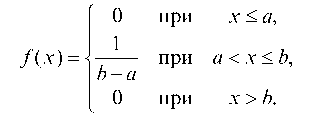
График равномерного распределения представлен на рис. 76.

Рис. 76

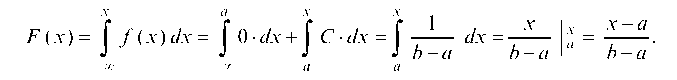
Найдем интегральную функцию:

х ах х 1

Б (х) = | / (х) dx = | 0 • dx + | С • dx = | - dx =

-¥ -¥ а а

Ее график представлен на рис. 77.

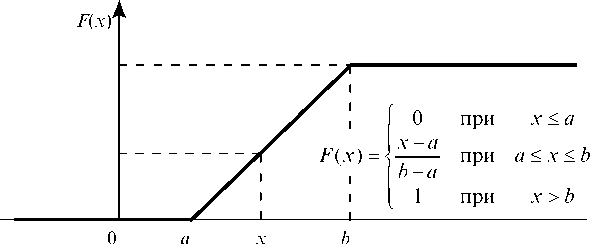
хУ

Рис. 77

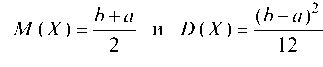
Для равномерного распределения:

М (X)=!ь+а и в(X)=(Ь-а)2

Пример 6.26. Мастер, осуществляющий ремонт на дому, может появиться в любое время с 10 до 18 часов. Клиент, прождав до 14 часов, отлучился на один час. Какова вероятность, что мастер (приход его обязателен) не застанет его дома?

Решение. Из анализа формулировки задачи принимаем равномерный закон распределения случайного времени прихода мастера. Для определения границ интервала времени учтем, что раз до 14 часов мастер не пришел, то до 18 часов он придет обязательно. Следовательно, а = 14 и b = 18, а интегральная функция распределения: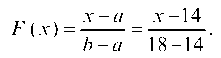

Тогда вероятность его появления в момент отсутствия клиента (с 14 до 15 часов) равна:

6.3.4.2. Экспоненциальное (показательное) распределение

Показательным (экспоненциальным) называется распределение вероятностей, которое описывается дифференциальной функцией: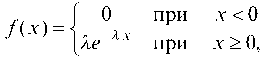

где I — постоянное положительное число.

Найдем интегральную функцию:

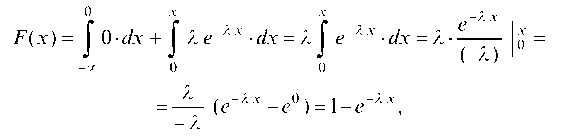
где l = const.

Вероятность безотказной работы на интервале времени от нуля до х*, соответствующей событию «появление отказа после t = х*»:

Пример 6.27. Построить графики интегральной и дифференциальной функций распределения для экспоненциального закона с параметром I = 0,7, для которого:

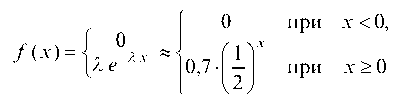
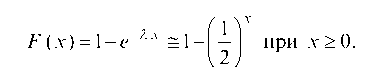
Графики этих функций изображены на рис. 78.

Пример 6.28. Радиосистема, имеющая 1000 элементов (с интенсивностью отказов Ii = 10-6 отк/ ч), прошла испытание и принята заказчиком. Требуется определить вероятность безотказной работы системы в интервале t1 < (t = t1 + D t) < t2, где D t = 1000 ч.

Решение. Интенсивность отказа системы из n = 1000 нерезервированных элементов, каждый из которых имеет Ii = 10-6 отк/ ч, равна Is = n ¦ Ii = 103 отк/ ч. При таких исходных данных вероятность отказа системы за время t = 1000 ч равна:

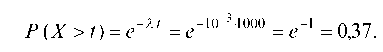
Пример 6.29. Холодильник имеет постоянную интенсивность отказа равную I = 105 отк/ ч. Какова вероятность, что он откажет после гарантийного срока t = 20000 часов?

Решение. Учитывая постоянную интенсивность отказов, можно принять экспоненциальный закон распределения вероятностей. Тогда вероятность отказа в интервале 0 < X < 20000 будет определяться с помощью интегральной функции:

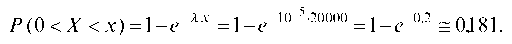
Очевидно, что вероятность отказа после гарантийного срока будет равна P (X > 20000) = 0,819.

Математическое ожидание непрерывной случайной величины, распределенной по экспоненциальному закону, равно величине, обратной параметру распределения:

а дисперсия: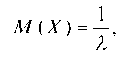

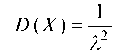
Преимущество этого распределения в том, что оно определяется одним параметром I, а обычно эти параметры бывают неизвестными и трудность заключается в том, чтобы их оценить.

Рассмотрим вероятность попадания случайной величины X в заданный интервал (a; b):

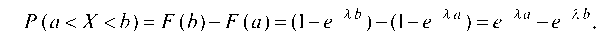
Итак,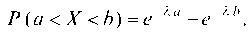

На практике очень часто имеют дело со случайными величинами, зависящими от большого числа сравнительно незначительных и взаимно независимых факторов.

Пример. При измерении длины материала, веса порции химиката и т. п. имеют место ошибки измерения. Найти вероятность, что ошибка лежит в пределах от - Dx до +Dх.

Плотность распределения такой случайной величины описывается кривой, представленной на графике (рис. 79), где x1 = x* - Dx и x2 = x* + D x. Это нормальный закон распределения.

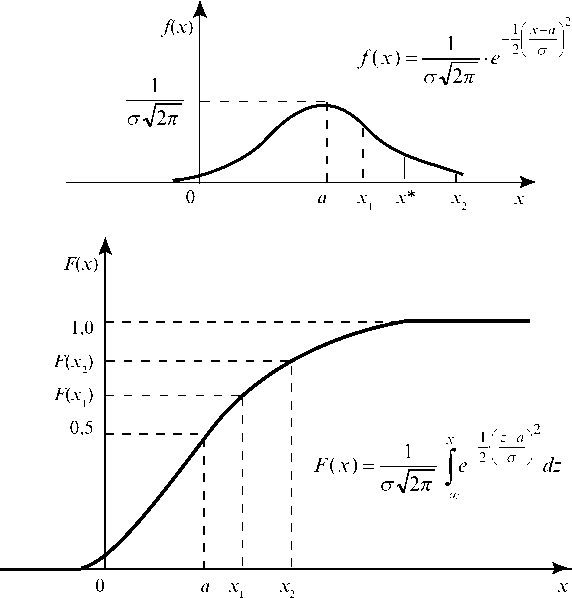
Рис. 79. График плотности (кривая Гаусса) и интегральная функция нормального закона распределения непрерывной случайной величины

Нормально распределенной называется случайная величина, имеющая в интервале от - да до +да плотность, определяемую формулой

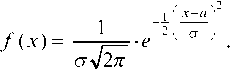
Ее интегральная функция:

При s = 1 и а = 0 будем иметь нормированное нормальное распределение

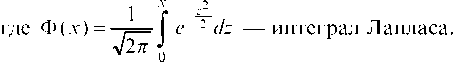
Указанный интеграл можно вычислить, пользуясь таблицами, и тогда вероятность попадания СВ X в интервал определяется по формуле

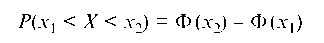
(Ф (-x) = - Ф (x) — нечетная функция).

Доказано, что переход от нормированной к обычной функции осуществляется подстановкой:

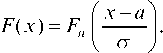
Пример 6.30. Случайная величина X распределена нормально. Математическое ожидание и среднее квадратическое отклонение этой величины соответственно равны 2 и 5. Найти вероятность того, что в результате испытания СВ X примет значение, принадлежащее интервалу (1; 4).

Решение. Воспользуемся формулой:

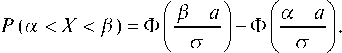
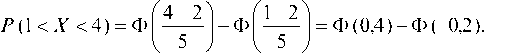
Так как функция Лапласа нечетная, то Ф (-0,2) = - Ф (0,2).

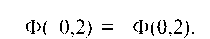
Таким образом,

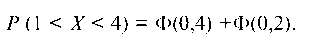
Р (1 < X < 4) = Ф(0,4) +Ф(0,2).

По таблице находим:

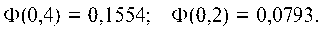
Ф (0,4) = 0,1554; Ф (0,2) = 0,0793.

Искомая вероятность равна:

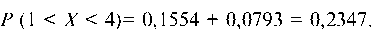
Р (1 < X < 4)= 0,1554 + 0,0793 = 0,2347.

Пример 6.31. Три непрерывные случайные величины имеют различные распределения: а) равномерное; б) экспоненциальное;

в) нормальное. Для всех трех распределений М (Хг) = ст(Х) = 4.

Найти для всех законов распределения вероятность того, что в результате испытания СВ Х1 примет значение, заключенное в интервале (5; 12).

Решение.

а) Равномерное распределение.

Дифференциальная функция равномерного распределения СВ Х1 имеет вид:

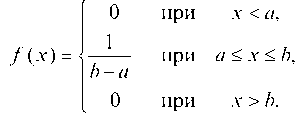
Параметры а и Ь найдем из условия, что для равномерного распределения

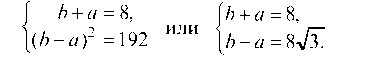
[(Ь - а)2 = 192 Решая эту систему, находим, что

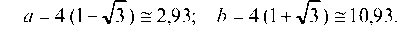
а = 4 (1 ->/3) @ 2,93; Ь = 4 (1 + >/3) @ 10,93.

При извлечении квадратного корня во втором уравнении системы взят знак «+» с учетом того, что а < Ь.

Имеем

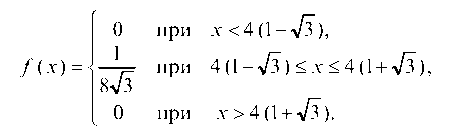
Вероятность попадания СВ Х1 в интервале (а; Р) определяем по формуле

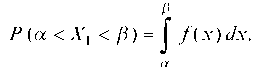
Для нашего случая искомая вероятность равна:

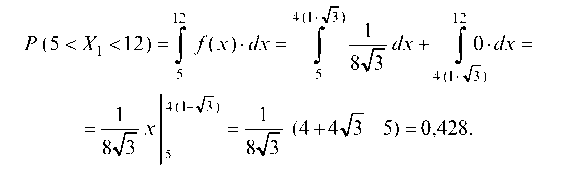
Итак,

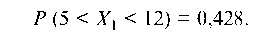
б) Экспоненциальное распределение.

Интегральная функция экспоненциального распределения СВ

Х2 имеет вид:

Известно, что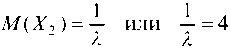По условию. Отсюда

Я = 0,25. Тогда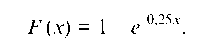

Искомая вероятность:

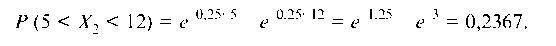
в) Нормальное распределение.

Вероятность того, что СВ X3, подчиненная нормальному закону распределения, попадет в интервал (a; b), равна:

Здесь Ф (х) — функция Лапласа, a — математическое ожидание, s — среднее квадратическое отклонение. Так как по условию задачи a = s = 4, то искомая вероятность равна:

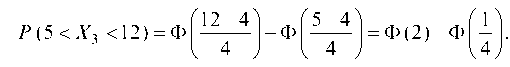
Находим по таблицам, что

Тогда

6.4. Основные понятия математической статистики

< Предыдущая		Следующая >