6.4.1. Генеральная совокупность. Выборка. Основные типы задач математической статистики

Пусть X — некоторая случайная величина (количественный признак). В дальнейшем все значения этой СВ будем называть генеральной совокупностью. Если, например, X — дискретная СВ, то генеральная совокупность — х1, х2, ..., xn.

Допустим, что в процессе наблюдений или опытов мы получили n значений (х1, х2, ..., xn) случайной величины X. В дальнейшем будем говорить, что сделали выборку х1, х2, ..., хп из генеральной совокупности X.

Число п называется объемом выборки.

Выборку х1, х2, ..., хп из генеральной совокупности X также можно представить, как значения п экземпляров х1, х2, ..., хп случайной величины X.

Заметим, что среди элементов выборки могут быть повторяющиеся. Поэтому для каждого элемента х. выборки говорят о частоте ее появления, т. е. сколько раз число х. наблюдалось в выборке.

В дальнейшем мы часто будем задавать выборку в виде таблицы

где х1, х2, ..., хт — различные элементы выборки, а п1, п2, ..., пт — частоты элементов выборки.

Ясно, что в этом случае объем выборки п = п1 + п2 + ... + пт. Значения х1, ..., хт выборки будем называть вариантами. Если варианты выборки расположены в возрастающем порядке, то выборка называется вариационным рядом.

Например,

Варианты выборки называются равноотстоящими, если X. +1 - X. = к, где к — постоянное число.

На практике при описании реальных процессов различные характеристики процесса являются случайными величинами. Поэтому возникают задачи определения законов распределения, математических ожиданий и других характеристик этих СВ, основываясь на изучении выборок.

Пусть значения СВ X определяют генеральную совокупность и Р(х) = Р (X < х) — интегральная функция распределения X. В дальнейшем мы будем ее называть теоретической функцией распределения генеральной совокупности X. Зная функцию Р (х), можно определить все характеристики СВ X. Поэтому поставим перед собой следующую задачу: можно ли с помощью выборок из генеральной совокупности X приближенно найти функцию Р (х)?

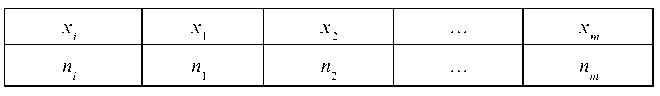
объема n = U1 + n2 + + nm

Построим функцию где nx — число вариантов

выборки, меньших х, т. е. — представляет относительную часто-

n

ту вариант выборки, меньших х. Функция F* (x) называется функцией распределения выборки или эмпирической функцией распределения.

Пример 6.32. Найти эмпирическую функцию по выборке

Решение. Найдем объем выборки: n = 10 + 15 + 25 = 50. Наименьшая варианта равна единице, следовательно, F* (x) = 0 при x < 1. Значение X = 4, а именно X1 = 1, наблюдалось 10 раз, следовательно,

Значения X < 6, а именно X1 = 1 и х2 = 4, наблюдались U1 + n2 = = 10 + 15 = 25 раз, следовательно,

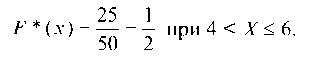
Так как х3 = 6 — наибольшая варианта, то

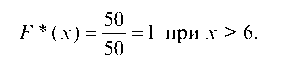
Значит,

Графически эта функция изображена на рис. 80.

Эмпирическая функция Р* (х) является приближением теоретической функции Р (х), и чем больше объем выборки п, тем точнее Р* (х) описывает Р (х) (по вероятности, т. е. случайные отклонения маловероятны).

В заключение заметим: эмпирическая функция обладает аналогичными свойствами, что и теоретическая функция распределения.

< Предыдущая		Следующая >