6.3.2. Числовые характеристики случайных величин

Математическое ожидание М (X) и дисперсия D (X) — наиболее часто применяемые характеристики случайной величины. Они характеризуют наиболее важные черты распределения: его положение и степень разбросанности.

Математическим ожиданием называется:

а) для дискретной случайной величины - сумма всех произведений ее возможных значений на их вероятности:

б) для непрерывных случайных величин:

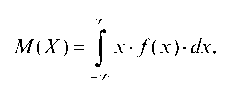
Здесь f (x) — дифференциальная функция распределения СВ.

Свойства математического ожидания (МО):

1. МО постоянной равно ей самой:

2. Постоянный множитель можно выносить за знак МО:

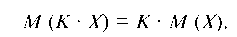
3. МО суммы двух случайных величин, являющихся функцией одного случайного события А, равно сумме математических ожиданий этих СВ:

4. МО произведения взаимно независимых случайных величин равно произведению их МО:

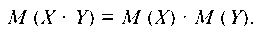
5. Свойства 3 и 4 можно распространить на любое число слагаемых или сомножителей.

Дисперсией случайной величины X называется математическое ожидание квадрата отклонения СВ от ее математического ожидания:

а) для дискретной СВ:

б) для непрерывной СВ:

Дисперсия равна разности между математическим ожиданием квадрата СВ X и квадратом ее математического ожидания, т. е.

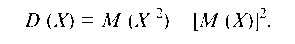
311

1. Дисперсия постоянной равна нулю:

2. Постоянный множитель можно выносит за знак дисперсии, возводя его в квадрат:

3. Дисперсия суммы или разности двух независимых СВ равна сумме их дисперсий:

4. Дисперсия суммы СВ с постоянной равна дисперсии СВ:

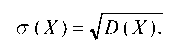
5. Свойства 3 и 4 можно распространить на любое число слагаемых.

Квадратный корень из дисперсии называется средним квадратическим отклонением случайной величины:

Использование s (X) полезно благодаря одинаковой размерности его с размерностью математического ожидания.

< Предыдущая		Следующая >