6.3.1. Законы распределения

Законом распределения вероятностей дискретной случайной величины называется любое правило, позволяющее находить все вероятности каждого значения этой величины. Для случайных величин любого вида — это правило, позволяющее находить вероятности появления этой величины в любом заданном интервале ее значений. Законы распределения задаются в аналитической, графической или табличной форме. Обычно для этого используются:

а) ряд распределения (многоугольник распределения);

б) интегральная функция распределения;

в) дифференциальная функция распределения.

Ряд распределения это таблица, в которой перечислены все возможные значения СВ и соответствующие им вероятности. Он является исчерпывающей характеристикой дискретной СВ.

У непрерывных СВ ряд распределения отсутствует, поэтому он не является универсальным законом распределения СВ. Пример ряда распределения иллюстрируется табл. 1, где представлено (в порядке возрастания) пять значений дискретной случайной величины X. При этом сумма всех вероятностей всегда равна единице.

Интегральной функцией распределения называют функцию F (x), определяющую для каждого значения х вероятность того, что случайная величина X примет значение, меньшее х, т. е.

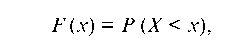
где х — некоторая текущая переменная.

Интегральная функция распределения — самая универсальная характеристика СВ. Она существует и для дискретных и для непрерывных СВ, полностью и однозначно характеризуя их с вероятностной точки зрения, т. е. является одной из форм закона распределения. Часто слово «интегральная» опускается.

Основные свойства интегральной функции распределения:

1. Функция распределения есть неотрицательная функция, заключенная между нулем и единицей: 0 < F (x) < 1, где на границах интервала: F (x = -<») = 0 и F (x = +¥) = 1.

2. Вероятность появления СВ в интервале от а до Д равна разности значений интегральной функции распределения на концах интервала, т. е.

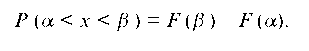
3. Интегральная функция — неубывающая функция своего аргумента, т. е. если x2 > x1, то F (x2) > F (x1).

4. В отдельных точках F (x) может иметь разрыв. В этих точках величина скачка функции распределения равна вероятности появления случайной величины в этой точке:

На рис. 72 представлена интегральная функция распределения дискретной случайной величины, заданной табл. 1.

307

5. График функции распределения дискретной СВ имеет ступенчатый вид (рис. 72), а непрерывной — непрерывную линию (рис. 73).

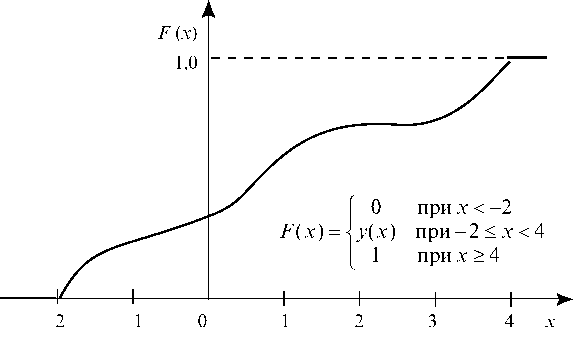
Рис. 73. Интегральная функция распределения непрерывной случайной величины

Плотностью (дифференциальной функцией) распределения непрерывной случайной величины x называется производная ее интегральной функции: f (x) = F (x).

Основные свойства плотности распределения:

1. Дифференциальная функция неотрицательна: f (x) > 0.

2. Интеграл от f (x) в пределах от - да до х* равен интегральной функции распределения

Этот интеграл численно равен площади фигуры, лежащей левее точки х* и заключенной между кривой плотности и осью абсцисс (рис. 74).

Рис. 74. Графическое изображение интегральной функции

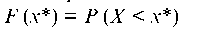
3. С помощью дифференциальной функции можно определить вероятность попадания случайной величины в заданный интервал от а до P, которая равна

т. е. вероятность попадания случайной величины X в заданный интервал (a; P) равна определенному интегралу от плотности распределения, взятому в пределах от а до P (см. рис. 75).

Рис. 75. Графическое изображение интегральной функции в интервале от а до P

4. Интеграл от плотности распределения в бесконечных пределах равен единице:

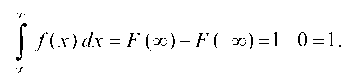
Пример 6.22. Случайная величина X задана интегральной функцией:

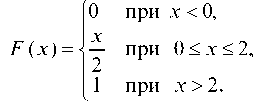
Найти вероятность того, что в результате испытания X примет значение, принадлежащее интервалу (0; 1).

Решение. Искомая вероятность равна приращению интегральной функции на заданном интервале:

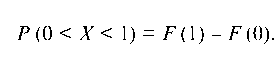
Так как на интервале (0; 1) по условию, то

Итак,

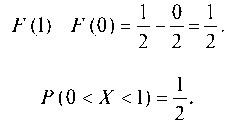
< Предыдущая		Следующая >