6.2. Схема повторных испытаний. 6.2.1. Формула Бернулли
Если при одних и тех же условиях определенный опыт повторяется n раз и если вероятность появления некоторого события А в каждом опыте равна р, то вероятность того, что событие А в серии из n опытов произойдет ровно к раз, находится по формуле Бернулли:

Сочетания из n по к находят по формуле
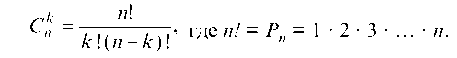
298
Число к появлений события А в серии из n опытов, вероятность которого наибольшая, называется наивероятнейшим числом наступления события А в n опытах. Это число находят по формуле
к = [np + р]. (2)
Символ [...] означает здесь целую часть числа.
Если число np + р - целое, то наивероятнейшим будет также и число к0 - 1 с той же вероятностью Pn (к0).
Пример 6.15. Среди деталей, обрабатываемых рабочим, бывает в среднем 4% нестандартных. Найти вероятность того, что среди взятых на испытание 30 деталей две детали будут нестандартными. Каково наивероятнейшее число нестандартных деталей в рассматриваемой выборке из 30 деталей и какова его вероятность?
Решение. Здесь опыт заключается в проверке каждой из 30 деталей на качество. Событие А - появление нестандартной детали; его вероятность Р = 0,04, тогда q = 0,96. Отсюда по формуле Бернулли находим:
P30 (2) = C0 (0,04)2 (0,96)28 » 0,202.
Наивероятнейшее число нестандартных деталей в данной выборке вычисляется по формуле (2):
к0 = [30 ¦ 0,04 + 0,04] = [1,24] = 1, а его вероятность равна
P30(1) = C1c • 0,041 • (0,96)29 » 0,305.
Пример 6.16. Вероятность попадания в цель при одном выстреле равна 0,8. Найти вероятность того, что в серии из четырех выстрелов будет: а) хотя бы одно попадание; б) не менее трех попаданий; в) не более одного попадания.
Решение. Здесь n = 4, p = 0,8, q = 0,2. а) Найдем вероятность противоположного события - в серии из четырех выстрелов нет ни одного попадания в цель:
Отсюда находим вероятность хотя бы одного попадания в цель:

б) Событие В, заключающееся в том, что в серии из четырех выстрелов произошло не менее трех попаданий в цель, означает, что было либо три попадания (событие С), либо четыре (событие D), т. е. В = С + D. Отсюда P (B) = P (C) + P (D); следовательно,
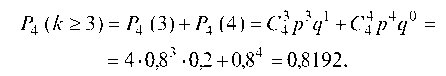
в) Аналогично вычисляется вероятность попадания в цель не более одного раза: 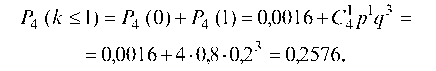
| < Предыдущая | Следующая > |
|---|