6.1.4. Формула полной вероятности и формула Байеса

Если с некоторым опытом связано n исключающих друг друга событий (гипотез) #1, -2, , —п и если событие А может осуществиться только при одной из этих гипотез, то вероятность события А вычисляется по формуле полной вероятности:

Если до опыта вероятности гипотез были P (H\), P (H2), ..., P (Hn), то после проведения опыта, в результате которого осуществилось событие А, вероятности гипотез можно переоценить по формуле Байеса:

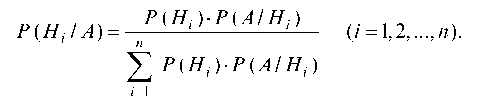
Пример 6.11. Имеется три урны с шарами. В первой урне 4 белых и 5 черных, во второй — 5 белых и 4 черных, в третьей — 6 белых шаров. Некто выбирает наугад одну из урн и вынимает из нее шар. Найти вероятность того, что: а) этот шар окажется белым; б) белый шар вынут из второй урны.

Решение:

а) пусть А — событие, означающее, что извлечен белый шар. Рассмотрим три гипотезы:

Так как урна, из которой извлекают шар, выбирается наугад, то

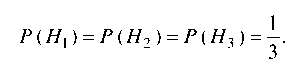
Условные вероятности события А соответственно равны:

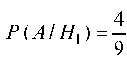(вероятность извлечения белого шара из первой урны),

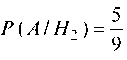(вероятность извлечения белого шара из второй урны), 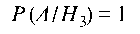(вероятность извлечения белого шара из третьей урны).

Отсюда по формуле полной вероятности получим:

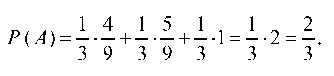
б) для определения вероятности того, что белый шар извлечен из второй урны, воспользуемся формулой Байеса:

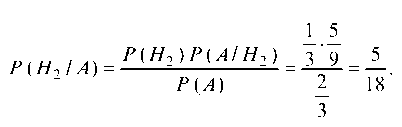
Пример 6.12. По линии связи передаются два сигнала А и В соответственно с вероятностями 0,72 и 0,28. Из-за помех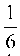Часть

А-сигналов искажается и принимается как В-сигналы, ачасть

переданных В-сигналов принимается как А-сигналы.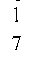

а) Определить вероятность того, что на приемном пункте будет принят А-сигнал.

б) Известно, что принят А-сигнал. Какова вероятность того, что он же и был передан?

Решение:

а) пусть событие А - на приемном пункте появился А-сигнал. Введем гипотезы: НА - передан сигнал А, НВ - передан сигнал В. По условию P (Ha) = 0,72; P (Hb) = 0,28.

Вероятность того, что принят А-сигнал при условии, что он же послан, равна: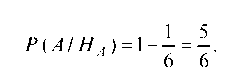

Вероятность того, что принят А-сигнал при условии, что послан В-сигнал, равна:

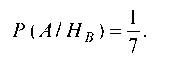
Отсюда по формуле полной вероятности получаем

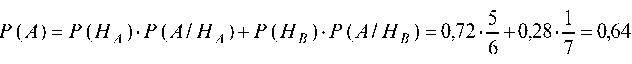
б) вероятность приема А-сигнала при условии, что он же был передан, найдем по формуле Байеса:

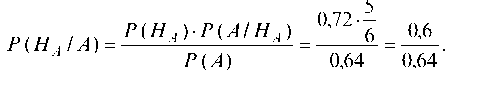
Пример 6.13. Пассажир может обратиться за получением билета в одну из трех касс. Вероятности обращения в каждую кассу зависят от их местоположения и равны соответственно Р1, Р2, Рз-Вероятность того, что к моменту прихода пассажира имеющиеся в кассе билеты будут распроданы, равна для первой кассы p4, для

второй - p5, для третьей - p6. Пассажир направился за билетом. Какова вероятность того, что он приобретет билет?

Решение. Рассмотрим следующие случайные события:

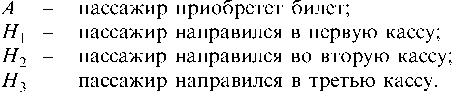
Ясно, что события -1, -2, -3 образуют полную группу событий и несовместны (мы считаем, что пассажир может направиться только в одну кассу). События -1, -2, —з являются гипотезами. Событие А может произойти только при условии, что произошла одна из гипотез.

По формуле полной вероятности:

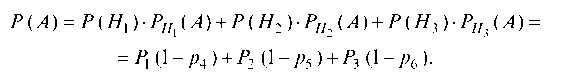
Пример 6.14. Имеются три партии деталей по 30 деталей в каждой. Число стандартных деталей в первой, второй и третьей партиях соответственно равно 20, 15, 10. Из наудачу взятой партии наудачу извлечена деталь, оказавшаяся стандартной. Затем из той же партии вторично наудачу извлекли деталь, которая также оказалась стандартной. Найти вероятность того, что детали были извлечены из третьей партии.

Решение. Обозначим через А событие — в каждом из двух испытаний была извлечена стандартная деталь.

Можно сделать три предположения (гипотезы): -1 — детали извлекались из первой партии; -2 — детали извлекались из второй партии; -3 — детали извлекались из третьей партии.

Так как детали извлекались из наудачу взятой партии, то вероятности гипотез одинаковы:

Найдем условную вероятность PH1 (A), т. е. вероятность того, что из первой партии будут последовательно извлечены две стандартные детали: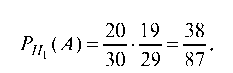

Найдем условную вероятность PH2 (Л), т. е. вероятность того, что из второй партии будут последовательно извлечены (без возвращения) две стандартные детали:

Найдем условную вероятностьТ. е. вероятность того,

что из третьей партии будут последовательно извлечены две стандартные детали:

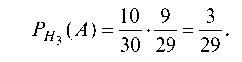
Искомая вероятность того, что обе извлеченные стандартные детали взяты из третьей партии, по формуле Бейеса равна:

< Предыдущая		Следующая >