6.1.3. Теоремы сложения и умножения вероятностей
Суммой нескольких событий называется событие, состоящее в появлении хотя бы одного из этих событий.
Произведением нескольких событий называется событие, состоящее в совместном осуществлении всех этих событий.
Теорема сложения вероятностей. Если события А1, А2, ... , Ап несовместны, т. е. никакие два из них не могут осуществиться вместе, то
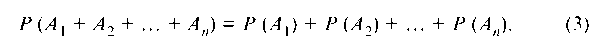
Вероятность события А, вычисленная в предположении, что произошло событие В, называется условной вероятностью события А при условии В и обозначается Р (А /В).
Теорема умножения вероятностей. Вероятность произведения нескольких событий равна произведению вероятности одного из них на условные вероятности всех остальных, причем вероятность каждого последующего события вычисляется в предположении, что все предыдущие события уже произошли:
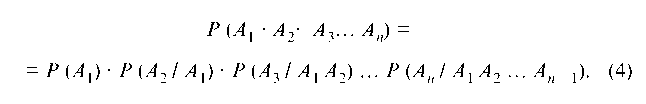
Если события А1, А2, ... , Ап независимы, т. е. осуществление любого числа из них не меняет вероятностей осуществления остальных, то
Пример 6.6. Два станка работают независимо друг от друга. Вероятность бесперебойной работы первого станка в течение некоторого времени t равна p1 = 0,9, второго — р2 = 0,8. Какова вероятность бесперебойной работы обоих станков в течение указанного промежутка времени?
Решение. Рассмотрим следующие события: А1 и А2 — бесперебойная работа соответственно первого и второго станков в течение времени t; A — бесперебойная работа обоих станков в течение указанного времени. Тогда событие А есть совмещение событий А1 и А2, т. е. А = А1 А2. Так как события А1 и А2 независимы (станки работают независимо друг от друга), то по формуле (5) получим:
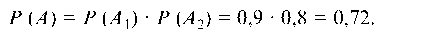
Пример 6.7. В задаче 6.6. определить вероятность бесперебойной работы хотя бы одного из двух станков в течение времени t (событие В).
Первый способ. Рассмотрим противоположное событие B означающее простой обоих станков в течение времени t. Очевидно, что событие B есть совмещение событий A1 и A2 — простоев первого и второго станков, т. е. B = A1A2. Так как события A и A2 независимы, то
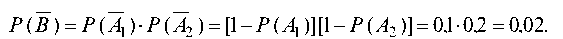
Отсюда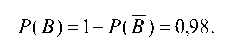
Второй способ. Событие В происходит в том случае, когда имеет место одно из следующих трех несовместных событий: либо
А1 ¦ А2 — совмещение событий А1 и А2 (первый станок работает,
второй — не работает), либо А1 ¦ А2 — совмещение событий А1 и А2 (первый станок не работает, второй - работает), либо А1 А2 — совмещение событий А1 и А2 (оба станка работают), т. е.
291
По формуле (3) получим:
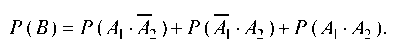
В силу того, что события А1 и А2, а следовательно, и А2 независимы, имеем: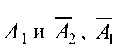
Пример 6.8. При увеличении напряжения может произойти разрыв электрической цепи вследствие выхода из строя одного из трех последовательно соединенных элементов; вероятности отказа элементов соответственно равны 0,2; 0,3; 0,4. Определить вероятность того, что разрыва цепи не произойдет.
Решение. Пусть события А1, А2, А3 означают выход из строя соответственно первого, второго и третьего элементов. Их вероятности по условию соответственно равны: P (A1) = 0,2; P (A2) = 0,3; P (A3) = 0,4. Тогда вероятности противоположных
событий A1, A2, A3 соответственно первый, второй и третий элемент не вышел из строя) равны:
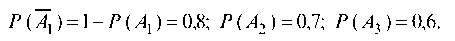
Событие А, состоящее в том, что разрыва цепи не произошло,
есть совмещение независимых событий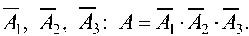
Следовательно, по формуле (5) получаем:
Пример 6.9. В урне 6 черных, 5 красных и 4 белых шара. Последовательно вынимают три шара. Найти вероятность того, что первый шар окажется черным, второй - красным и третий - белым.
Решение. Рассмотрим следующие события: А — первый вынутый шар черный, Б — второй шар красный, С — третий шар белый. Обозначим через D событие, заключающееся в том, что шары вынуты в последовательности: черный, красный, белый. Очевидно, D = A ¦ B ¦ C.
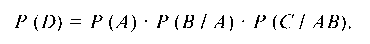
Р (Б) = Р (А) ¦ Р (В / А) ¦ Р (С / АВ).
Найдем вероятности, входящие в правую часть этого равенства. Вероятность того, что первоначально вынут черный шар,
6 2
Р (А) - и - 5. Вероятность извлечения из урны красного шара при условии, что первоначально был вынут черный шар, Р (В/ А) -14, так как после изъятия черного шара в урне осталось 14 шаров и из них — 5 красных. Вероятность извлечения из урны белого шара после того, как были извлечены черный и крас-
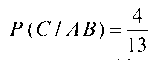
4
ный шары, Р (С / АВ) -13 (после изъятия черного и красного
шаров в урне осталось 13 шаров и из них — 4 белых).
Таким образом,
Р ( б ) - 2 • — • — - —.
5 14 13 91
Пример 6.10. Завод изготавливает определенного типа изделия; каждое изделие имеет дефект с вероятностью р1 = 0,1. Изделие осматривается одним контролером; он обнаруживает имеющийся дефект с вероятностью р2 = 0,8, а если дефект не обнаружен, пропускает изделие в готовую продукцию. Кроме того, контролер может по ошибке забраковать изделие, не имеющее дефекта; вероятность этого равна р3 = 0,3. Найти вероятности следующих событий:
А1 - изделие будет забраковано, но ошибочно;
А2 - изделие будет пропущено в готовую продукцию с дефектом;
А3 - изделие будет забраковано.
Решение. Рассмотрим следующие события:
В1 - изделие имеет дефект;
В2 - контролер обнаружит имеющийся дефект;
В3 - контролер забракует изделие, не имеющее дефекта.
По условию задачи Р (В1) = р1 = 0,1; Р (В2) = р2 = 0,8; Рв1 (В3) - р3 - 0,3. Событие А1 по смыслу означает: «изделие не
имеет дефекта и изделие будет забраковано контролером», т. е. Тогда
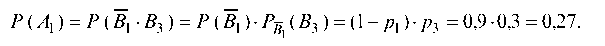
Событие А2 по смыслу означает: «изделие имеет дефект и контролер не обнаружит дефект», т. е. A2 = B1 • B2. Тогда
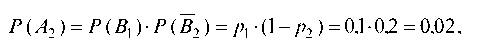
т. к. события B и B2 независимые.
Событие А3 по смыслу означает: «изделие имеет дефект и контролер обнаруживает дефект или изделие не имеет дефекта и контролер забракует изделие», т. е.
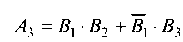
и
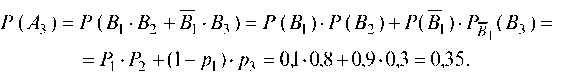
| < Предыдущая | Следующая > |
|---|
