6.1.2. Геометрические вероятности

Если результат испытания определяется случайным положением точки в некоторой области, причем положения точек в этой области равновозможны, то вероятность события находится по формуле

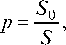
где S - геометрическая мера (длина, площадь или объем) всей области, S0 - геометрическая мера той части области, попадание в которую благоприятствует данному событию.

Пример 6.3. В круг вписан квадрат. Какова вероятность того, что точка, наудачу поставленная в круге, окажется внутри квадрата?

2

Решение. Площадь круга S = т, площадь квадрата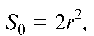 где r - радиус круга (рис. 69). Отсюда по формуле (2) находим искомую вероятность:

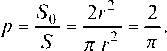
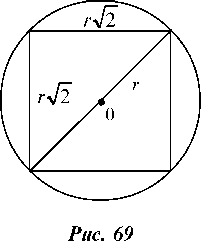
Рис. 69

Пример 6.4. Известно, что телефонный звонок должен последовать от 11 ч до 11 ч 30 мин. Какова вероятность того, что звонок произойдет в последние 10 минут указанного промежутка, если момент звонка случаен?

Решение. Воспользуемся геометрической схемой. Для этого промежуток времени от 11 ч до 11 ч 30 мин представим в виде отрезка АВ длиной в 30 единиц, а промежуток времени от 11 ч 20 мин до 11 ч 30 мин - в виде отрезка СВ длиной в 10 единиц (рис. 70). Слу-

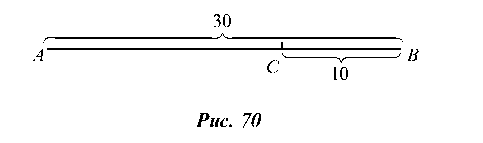
чайный звонок в некоторый момент рассматриваемого получаса изображается наугад взятой точкой на отрезке АВ. Тогда вероятность того, что звонок произойдет в интервале от 11 ч 20 мин до

11 ч 30 мин, в полученной схеме означает вероятность того, что точка, наугад взятая на отрезке АВ, окажется принадлежащей отрезку СВ. Эта вероятность, очевидно, равна:

Пример 6.5. В любой момент времени промежутка Т равновозможны поступления в приемник двух сигналов. Приемник считается забитым, если разность по времени между сигналами меньше t < T. Какова вероятность того, что приемник будет забит?

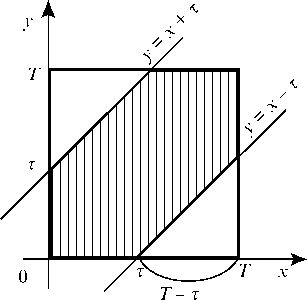
Решение. Рассмотрим прямоугольную декартову систему координат хОу. Пусть х и у - моменты поступления в приемник соответственно первого и второго сигналов. Тогда все возможные комбинации поступления сигналов изобразятся точками квадрата 0 < х < Т, 0 < у < Т. Так как моменты поступления сигналов равновозможны в течение промежутка времени Т, то положения точек (х; у) в области рассматриваемого квадрата также равновозможны.

Выясним, какие точки квадрата благоприятствуют интересующему нас событию А (приемник забит). Событие А может произойти лишь в том случае, если разность по времени между сигналами будет меньше t т. е. если

Таким образом, область квадрата, благоприятствующая событию А (на рис. 71 она заштрихована), состоит из точек, координаты (х; у) которых удовлетворяют неравенству (*).

2

Площадь квадрата S = T ; площадь заштрихованной области

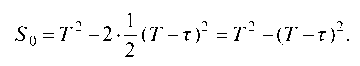
Отсюда

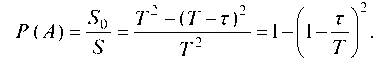
< Предыдущая		Следующая >