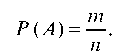6.1. Основные понятия и теоремы теории вероятностей. 6.1.1. Классическое определение вероятности

6.1.1. Классическое определение вероятности

Если испытание может привести к одному и только к одному из n различных равновозможных исходов (называемых элементарными исходами) и если m из этих исходов благоприятствуют появлению событий А, то вероятность события А определяется формулой

(1)

Это — классическое определение вероятности.

Отметим основные свойства вероятности.

1. Вероятность любого события заключена между нулем и единицей: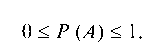

2. Вероятность достоверного события I, т. е. такого события, которое при испытании обязательно произойдет, равна единице:

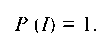
3. Вероятность невозможного события О, т. е. события, которое в результате испытания не может произойти, равна нулю:

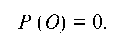
4. Сумма вероятностей двух противоположных событий А и

А, т. е. таких событий, что появление одного из них исключает появление другого, равна единице:

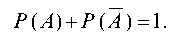
Пример 6.1. Из урны, в которой находится 4 белых, 9 черных и 7 красных шаров, наугад вынимают один шар. Какова вероятность появления белого шара?

Решение. Здесь элементарным исходом является извлечение из урны любого шара. Число всех таких исходов равно числу шаров в урне, т. е. n = 20. Число исходов, благоприятствующих появлению белого шара (событие А), очевидно, равно числу белых шаров в урне, т. е. m = 4. Поэтому по формуле (1) находим:

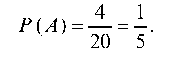
Пример 6.2. Игральный кубик бросают два раза. Какова вероятность того, что сумма выпавших очков окажется равной восьми?

Решение. Обозначим через Aj событие, состоящее в том, что при первом подбрасывании выпало i очков, а при втором - j оч-

можно рассматривать как элементарные исходы опыта. Следовательно, число всех элементарных исходов n = 36. Появлению события А (сумма выпавших очков равна восьми) благоприятствуют исходы А26, А35, А44, А53, А62. Таким образом, m = 5. Отсюда получаем:

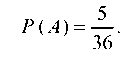
< Предыдущая		Следующая >