5.7. Приложение рядов к приближенным вычислениям

Пример 5.24. Вычислить sin 18°, ограничиваясь первыми двумя членами ряда (3), и оценить получающуюся при этом погрешность.

Решение. Так как разложение sin x в ряд Тейлора справедливо при любом х, то, в частности, при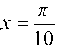Имеем

Полученный ряд — знакочередующийся. Ограничиваясь двумя

. п

членами этого ряда, т. е. считая sin— равным их сумме, мы тем самым допускаем ошибку, не превосходящую первого отбрасы-

ваемого члена - (см. 5.3). Так как, то с точно

стью до 0,0001 получаем

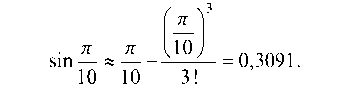
2

Пример 5.25. Вычислить e с точностью до 0,01.

Решение. Пользуясь разложением (2), при х = 2 получим

Остается решить вопрос о том, сколько членов данного ряда надо взять, чтобы получить значение е2 с требуемой точностью. Пусть искомое число членов равно к. Это означает, что ошибка

DSk, которую мы допускаем, заменяя сумму ряда его k-й частичной суммой, равна сумме членов ряда, начиная с (k + 1)-го:

Если в этом ряде заменить каждое из чисел k + 2, k + 3, . числом k + 1, то знаменатели дробей уменьшатся, а сами дроби, следовательно, увеличатся. Отсюда

и следовательно, равно

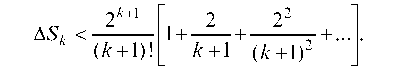
Выражение, стоящее в квадратной скобке, есть сумма членов бесконечно убывающей геометрической прогрессии со знаменателем

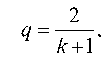
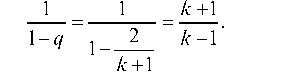
Таким образом,

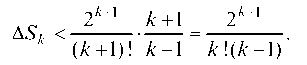
Но с другой стороны, ошибка DSk не должна превосходить 0,01: DSk < 0,01. Решая методом подбора неравенство

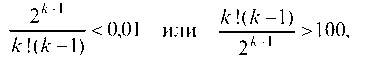
получим k > 7.

Итак, для достижения требуемой точности надо взять 8 членов ряда:

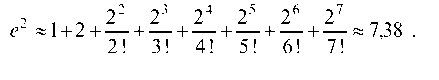
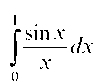
Решение. Данный определенный интеграл можно вычислить только приближенно. Для этого разложим подинтегральную функцию в ряд Тейлора:

Отсюда

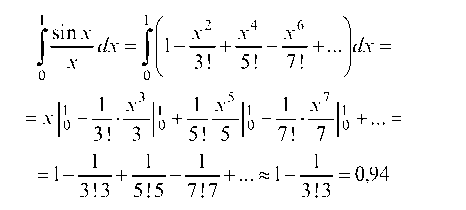
(здесь мы ограничились двумя первыми членами этого знакопеременного ряда, так как третий член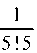Меньше 0,01).

< Предыдущая		Следующая >