5.6. Разложение функций в степенные ряды Тейлора
Рядом Тейлора для функции f (x) называется степенной ряд вида

При представлении элементарной функции в виде суммы ряда Тейлора обычно поступают следующим образом: вычисляют последовательные производные данной функции в точке х = 0, а затем, пользуясь формулой (1), составляют для нее ряд Тейлора и определяют интервал сходимости полученного ряда. В этом интервале ряд Тейлора сходится к породившей его функции f (x), если только все значения f (0), f (0), ..., f (n)(0), ... получаются непосредственной подстановкой значения х = 0 в выражения f (х), f' (х), ...,f<%), ... .
Применяя рассмотренный способ, можно найти разложение в ряд Тейлора для следующих функций:
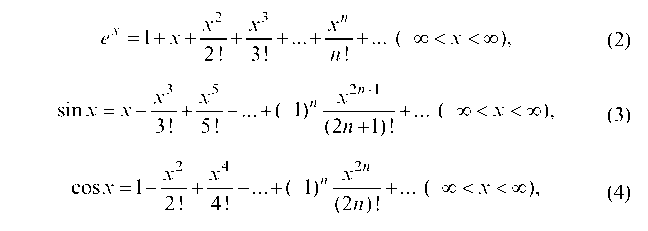
Решение. Имеем Отсюда
Отсюда

220

Помимо указанного способа, можно получить разложения функций в ряд Тейлора, исходя из известных разложений, например, разложений (2) - (7). При этом возможно использование следующих действий над степенными рядами внутри их интервалов сходимости:
1) два степенных ряда можно почленно складывать и умножать по правилу умножения многочленов;
2) степенной ряд можно почленно умножать на общий множитель;
3) степенной ряд можно почленно интегрировать и дифференцировать любое число раз.
Так как степенной ряд для своей суммы есть ряд Тейлора, то полученное в результате указанных действий разложение будет искомым.
Пример 5.20. Разложить в ряд Тейлора функцию f (x) = e3x.
Решение. Вычислим значения данной функции и ее последовательных производных при х = 0:
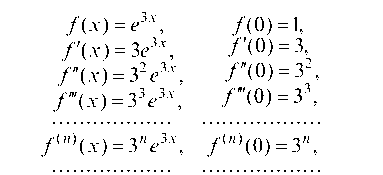
Подставляя полученные значения в общее выражение ряда Тейлора для произвольной функции, получим
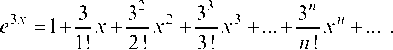
Это и есть разложение в ряд Тейлора для функции f (x) = e3x. Полученный ряд сходится к породившей его функции f (x) = e3x при любом значении х (см. задачу 5.19).
Заметим, что то же самое разложение можно получить из ряда Тейлора для функции e3x заменой х на 3х.
Пример 5.21. Разложить в ряд Тейлора функциюf (x) = In (1 - 2x). Решение. Заменяя в разложении (7) х на -2х, получим:

или

Разложение (7) справедливо в интервале -1 < x < 1, а искомое разложение получается в результате замены х на -2х; следовательно, для нахождения интервала сходимости полученного ряда нужно решить неравенство

откуда
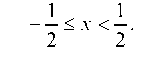
Пример 5.22. Разложить в ряд Тейлора функцию f (x) = cos 2x. Решение. По известной тригонометрической формуле имеем:
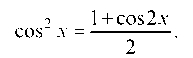
Разложим в ряд Тейлора функцию cos 2x, заменяя в разложении (4) х на 2х:

или
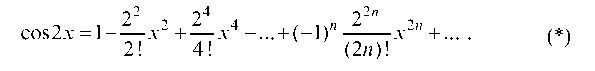
222
Разложение (4) справедливо при любом х, поэтому ряд Тейлора для cos 2x сходится к породившей его функции также на всей числовой оси.
Для того чтобы получить разложение в ряд Тейлора функции  Умножим все члены ряда (*) на
Умножим все члены ряда (*) на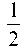 ¦:
¦:

Тогда
Это и есть разложение в ряд Тейлора функции f (x) = cos2 x. Очевидно, что оно справедливо при любом х.
Пример 5.23. Применяя дифференцирование и интегрирование, найти разложение в ряд Тейлора для данной функцииf (x) = arc tg x и указать интервалы, в которых эти разложения имеют место.
Решение. Запишем выражение данной функции в виде интеграла:

Разложим подинтегральную функцию В ряд Тей
В ряд Тей
лора. Для этого в разложении (6) заменим х на - t2:

Очевидно, что этот ряд сходится в интервале (-1; 1). Интегрируя почленно полученный ряд в пределах от 0 до х (где | x | < 1), получаем разложение функции f (x) = arctg x в ряд Тейлора:

Этот ряд сходится в том же интервале (-1; 1), что и исходный ряд.
| < Предыдущая | Следующая > |
|---|