5.5. Степенные ряды

Степенным рядом называется ряд вида

где A1, а2, а3, ап... - постоянные числа, называемые коэффициентами ряда.

Областью сходимости степенного ряда называется совокупность всех значений х, при которых данный ряд сходится. Нахождение области сходимости состоит из двух этапов.

1. Определяется интервал сходимости степенного ряда, т. е. интервал (-R, R) числовой оси, симметричный относительно точки х = 0 и обладающий тем свойством, что при всех | x | < R ряд сходится и притом абсолютно, а при всех | x | > R - ряд расходится. Для этого применяется признак Даламбера к ряду

члены которого есть абсолютные величины членов данного ряда (1).

2. Исследуется сходимость ряда (1) на концах интервала сходимости в точках x = - R и x = R.

Пример 5.16. Исследовать сходимость ряда

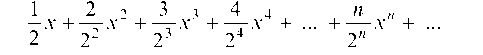
в точках x = 1, x = 3, x = -2.

Решение. При х = 1 данный ряд превращается в числовой ряд

217

который расходится (так как не выполняется необходимый признак сходимости ряда).

Пример 5.17. Найти область сходимости степенного ряда

Решение. Составим ряд из абсолютных величин членов данного ряда:

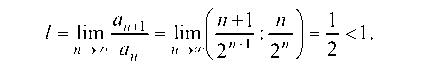
При х = 3 имеем ряд

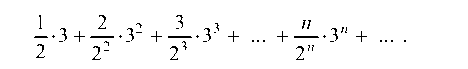
Применяя признак Даламбера, получим

Следовательно, в точке х = 3 данный ряд расходится. Наконец, при х = -2 получаем следующий числовой ряд:

Согласно признаку Даламбера полученный знакоположительный ряд сходится (абсолютно) при тех значениях х, для которых

Определим, при каких значениях х этот предел I будет меньше единицы. Для этого решим неравенствоИли | x | < 2, отку

да -2 < x < 2.

Таким образом, первоначальный ряд сходится (абсолютно) в интервале (-2; 2) — это и есть интервал сходимости данного ряда. Исследуем сходимость ряда на концах интервала сходимости. При х = -2 получаем числовой ряд

Это — гармонический ряд, который, как известно, расходится. При х = 2 получаем числовой знакочередующийся ряд

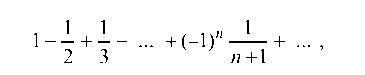
который по признаку Лейбница сходится (условно).

Итак, область сходимости данного ряда -2 < x < 2.

Пример 5.18. Найти область сходимости степенного ряда

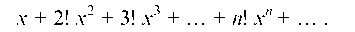
Решение. Здесь Отсюда

т. е.

Таким образом, согласно признаку Даламбера ряд сходится только в точке х = 0.

Пример 5.19. Найти область сходимости степенного ряда

219

Следовательно, при любом конечном х по признаку Даламбера данный ряд абсолютно сходится. Область сходимости рассматриваемого ряда есть вся числовая ось.

< Предыдущая		Следующая >