5.4. Абсолютная и условная сходимость знакопеременного ряда

Ряд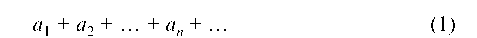

называется знакопеременным, если среди его членов имеются как положительные, так и отрицательные числа.

Признак сходимости знакопеременного ряда. Если ряд

составленный из абсолютных величин членов рядов (1), сходится, то ряд (1) также сходится.

Знакопеременный ряд (1) называется абсолютно сходящимся, если сходится ряд (2), составленный из абсолютных величин членов данного ряда (1).

Сходящийся знакопеременный ряд называется условно сходящимся, если ряд, составленный из абсолютных величин его членов, расходится.

Пример 5.12. Исследовать на сходимость ряд

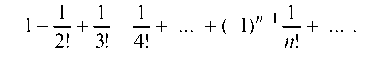
Решение. Рассмотрим ряд, составленный из абсолютных величин членов данного ряда:

По признаку Даламбера этот ряд сходится, так как

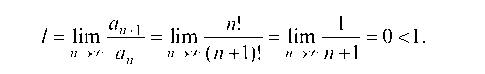
Следовательно, первоначальный ряд является абсолютно сходящимся.

Пример 5.13. Исследовать на сходимость ряд

он содержит как положительные члены

так и отрицательные Ряд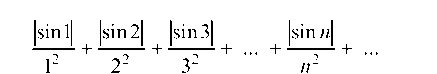

сходится, так как его члены не превосходят соответствующих членов сходящегося ряда

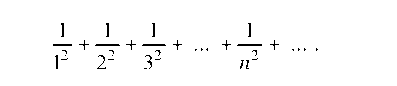
Следовательно, исходный ряд сходится абсолютно.

Пример 5.14. Исследовать на сходимость ряд

Решение. Ряд

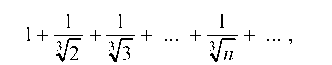
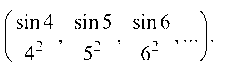
составленный из абсолютных величин членов данного ряда, расходится (см. задачу 5.5). Следовательно, ряд (*) не является абсолютно сходящимся. Остается выяснить, сходится ли он (условно) или расходится. Рассматриваемый ряд — знакочередующийся. Поэтому для решения вопроса о его сходимости можно воспользоваться признаком Лейбница. Так как члены ряда по абсолютной

величине монотонно убывают:И общий член стре

мится к нулю: lim ап = 0, то ряд (*) сходится. Итак, данный ряд

П®¥

сходится условно.

Пример 5.15. Исследовать на сходимость ряд

Решение. Данный знакопеременный ряд расходится, так как для него не выполняется необходимый признак сходимости:

lim an = lim sin np — не существует.

п®¥ n®¥ 3

< Предыдущая		Следующая >