5.0. Ряды 5.1. Основные понятия

Числовым рядом называется выражение вида:

где числа а1, а2, а3, ... ап, называемые членами ряда, образуют бесконечную последовательность.

Ряд называется сходящимся, если последовательность его частичных сумм

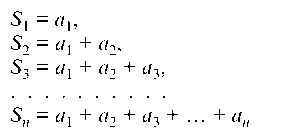
при п ® ¥ имеет конечный предел:Этот предел назы

вается суммой сходящегося ряда. Если конечный пределне

существует, то ряд называется расходящимся.

Пример 5.1. Написать пять первых членов последовательности, если ее n-й член ап имеет вид:

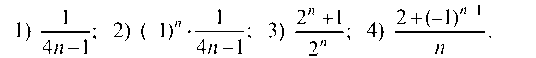
Решение. Вместо п подставляем 1, 2, ..., 5:

Пример 5.2. Пользуясь непосредственно определением, показать что ряд сходится, и найти его сумму.

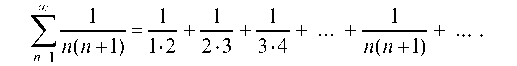
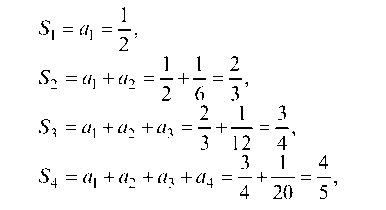
Решение. По определению частичной суммы ряда имеем:

Таким образом, получаем следующую последовательность частичных сумм:

общий член которой равен: П. Ясно, что эта последовательность сходится и ее предел равен единице:

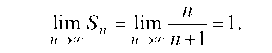
lim Sn = lim —n— = 1.

Это означает, что данный ряд сходится и сумма его равна единице.

< Предыдущая		Следующая >