4.8. Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами
Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами имеет вид:

у" + ру' + ду=/ (х). (1)
Оно отличается от соответствующего линейного однородного уравнения

у" + ру' + ду = 0. (2)
наличием в правой части некоторой функции / (х).
200
Для нахождения общего решения уравнения (1) сначала нужно найти общее решение у уравнения (2), а затем найти какое-либо частное решение у* уравнения (1). Их сумма есть общее решение данного неоднородного уравнения (1):
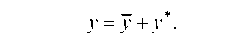
Приведем правило отыскания частного решения у* уравнения (1) в следующих двух случаях: правая часть f (x) имеет вид

f (x) = ekxP„(x). (3)
где Pn(x) — многочлен степени n; правая часть f (x) имеет вид
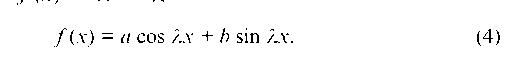
f (x) = a cos 1x + b sin 1x. (4)
Рассмотрим каждый из этих случаев в отдельности.
I. Пусть правая часть уравнения (1) имеет вид
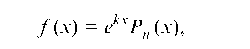
f (x) = (xX
причем число k не является корнем характеристического уравнения

r2 + p + q = 0, (5)
соответствующего однородному уравнению (2). Тогда частное решение уравнения (1) следует искать в форме

у* = e„(x), (6)
где Qn(x) — некоторый многочлен той же степени n с неопределенными коэффициентами.
Если же число к является корнем характеристического уравнения (5), то частное решение уравнения (1) следует искать в форме
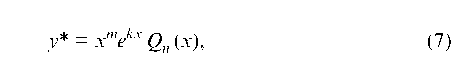
у* = xmekx Q (x), (7)
где m — кратность корня к (т. е. m = 1, если к — однократный корень, и m = 2, если к — двукратный корень).
II. Пусть теперь правая часть уравнения (1) имеет вид:
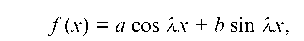
причем числа ±1i не являются корнями характеристического уравнения (5). Тогда частное решение уравнения (1) следует искать в форме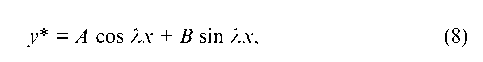
где А и В — неопределенные коэффициенты.
Если же комплексные числа ±1i являются корнями характеристического уравнения (5), то частное решение уравнения (1) следует искать в форме
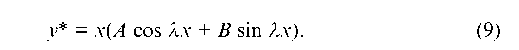
Пример 4.21. Найти общее решение уравнения 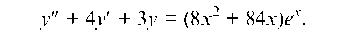 Решение:
Решение:
1. Найдем общее решение у соответствующего однородного уравнения
Решая отвечающее ему характеристическое уравнение  получаем корни r1 = -3, r2 = -1. Следовательно,
получаем корни r1 = -3, r2 = -1. Следовательно,
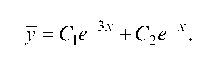
2. Перейдем к отысканию частного решения у* данного уравнения. Здесь правая часть f (x) = (8x2 + 84x)ex имеет вид (3): n = 2, P2(x) = 8x2 + 84x, k = 1, причем k = 1 не является корнем характеристического уравнения. Следовательно, частное решение у* нужно искать в форме

где A, B и C — некоторые коэффициенты, подлежащие определению. Для их отыскания воспользуемся тем, что у* должно быть решением данного уравнения. Найдем у*' и у*":

теперь подставим выражения для у*, у*' и у*" в данное уравнение:
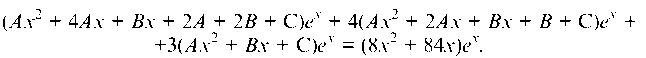
Сокращая обе части полученного равенства на ex и группируя члены при одинаковых степенях x, в результате получим

Это равенство выполняется тождественно только в том случае, когда коэффициенты при одинаковых степенях x в обеих частях равенства равны между собой.
Итак, имеем следующую систему уравнений для отыскания коэффициентов A, В и С:
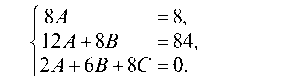
Решая эту систему, найдем A = 1, В = 9, С = -7. Таким образом, получаем искомое частное решение
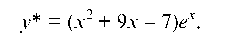
Теперь можно записать общее решение данного уравнения

Пример 4.22. Найти общее решение уравнения
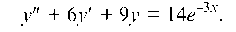
Решение. 1. Найдем у.
Характеристическое уравнениеимеем корни
r = r = -3. Следовательно,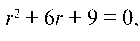
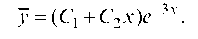
203
2. Найдем теперь у*. Здесь правая часть имеет вид (3): n = 0, P0 = 14, к = -3. Так как к = -3 является двукратным корнем характеристического уравнения, то частное решение у* следует искать в форме
у* = Ax2e-3x,
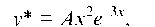
где A — коэффициент, подлежащий определению. Вычислим производные у*' и у*":
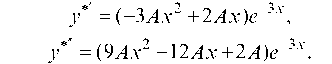
у* = (-3Ax2 + 2 Ax )e-3x, у*' = (9Ax2 -12Ax + 2A)e-3x.
Подставляя выражения для у*, у*' и у*" в данное уравнение, сокращая обе его части на e-3x и приводя подобные члены, в итоге получим 2A = 14, откуда A = 7. Следовательно, искомое частное решение имеет вид:

у* = 7x2e-3x.
Итак, общее решение данного уравнения
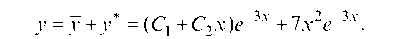
у = у + у* = (C1 + C2 x )e-3x + 7x2 e-3x.
Пример 4.23. Найти общее решение уравнения у" - 4у' + 5у = 2 cos x + 6 sin x.

Решение. 1. Найдем у. Характеристическое уравнение r2 - 4r + 5 = 0

имеем корни Г1 2 = 2 ± i. Следовательно,

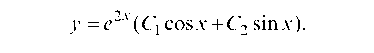
у = e2x(C1cosx + C2 sinx).
2. Будем теперь искать у*. Здесь правая часть f (x) имеет вид (4): а = 2, b = 6, l = ± i. Числа ± i не являются корнями характеристического уравнения, поэтому частное решение у* следует искать в форме
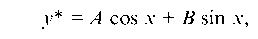
где A и В — неопределенные коэффициенты. Найдем производные у*' и у*":
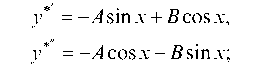
подставляя теперь выражения для у*, у*' и у*" в данное уравнение и группируя члены при cos x и sin x, в результате получим

Следовательно, для нахождения A и В имеем систему

откуда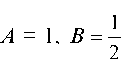 . Таким образом,
. Таким образом,
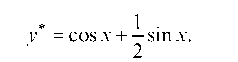
Итак, общее решение данного уравнения имеет вид:
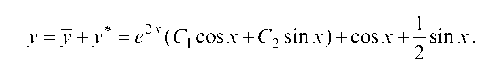
Пример 4.24. Найти общее решение уравнения
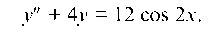
Решение. 1. Найдем сначала у. Характеристическое уравнение г2 + 4 = 0, имеет корни Г1 2 = ± 2г. Следовательно,
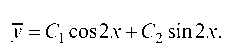
2. Переходим к нахождению у*. Здесь правая часть f (x) имеет вид (4): а = 12, b = 0, I = ± 2г. Так как числа ± 2г являются корнями характеристического уравнения, то частное решение следует искать в форме
Подставив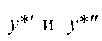 В данное уравнение и приведя подобные
В данное уравнение и приведя подобные
члены, получим

откуда

т. е. Поэтому
Поэтому
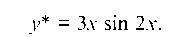
Итак, общее решение
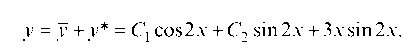
Пример 4.25. Найти частное решение уравнения 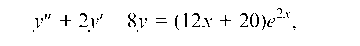 удовлетворяющее начальным условиям у (0) = 0, у' (0) = 1.
удовлетворяющее начальным условиям у (0) = 0, у' (0) = 1.
2
Решение. 1. Характеристическое уравнение r + 2т - 8 = 0 имеет корни T1 = -4, т2 = 2. Следовательно,

где А и В — неопределенные коэффициенты. Имеем
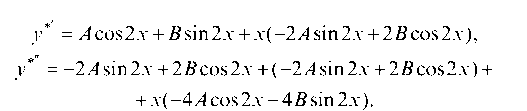
2. Правая часть данного уравнения имеет вид (3): n = 1,  Так как к = 2 является однократным корнем характеристического уравнения, то частное решение у* ищем в форме
Так как к = 2 является однократным корнем характеристического уравнения, то частное решение у* ищем в форме
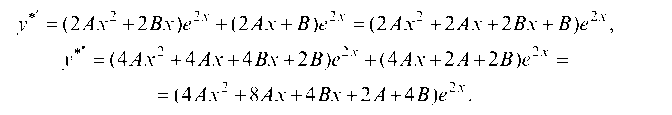
Подставляя у*, у*' и у*" в данное уравнение, сокращая обе его одя подобные члены, оконч
части на е2х и приводя подобные члены, окончательно получим
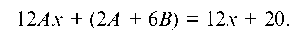
12Ах + (2А + 6В) = 12х + 20.
Решая систему

Г12 А = 12,
{ 2 А + 6В = 20,
находим А = 1, В = 3. Отсюда
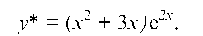
у* = (х2 + 3х)е2х.
Итак, найдено общее решение данного уравнения

у = у + у* = С1е-4х + С2 е2 х + (х2 + 3х)е2х.
3. Для нахождения искомого частного решения воспользуемся заданными начальными условиями. Найдем производную общего решения

у' = -4С1е-4х + 2С2е2х + (2х2 + 8х + 3)е2х;
подставив в выражения для общего решения и его производной значения х = 0, у = 0, у' = 1, получим систему уравнений для нахождения С1 и С2:
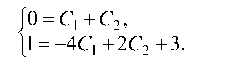
0 = С1 + С2,
1 = -4С1 + 2С2 + 3.
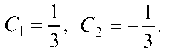
Отсюда С1 = 3, С2 = - 1. Таким образом, искомое частное решение имеет вид;
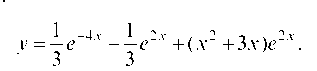
у = I е-4х -1 е2х + (х2 + 3х)е2х.
| < Предыдущая | Следующая > |
|---|