5.2. Необходимый признак сходимости ряда. Достаточные признаки сходимости рядов с положительными членами
Ряд может сходиться только при условии, что его общий член ап при неограниченном увеличении номера n стремится к нулю:
lim an - 0 - это необходимый признак сходимости ряда.
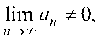
Если же lim an ф 0, то ряд расходится - это достаточный при-
знак расходимости ряда.
Для знакоположительных числовых рядов имеют место следующие достаточные признаки, по которым можно установить их сходимость или расходимость.
1. Признак сравнения. Если члены знакоположительного ряда
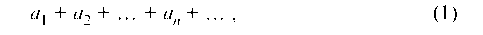
начиная с некоторого номера, не превосходят соответствующих членов ряда
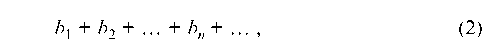
то из сходимости ряда (2) следует сходимость ряда (1), а из расходимости ряда (1) следует расходимость ряда (2).
При исследовании рядов на сходимость и расходимость по этому признаку часто используется геометрическая прогрессия

которая сходится при | q | < 1 и расходится при | q | > 1, и гармонический ряд
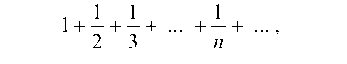
являющийся расходящимся рядом.
2. Признак Даламбера. Если для ряда (1)
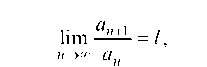
то при I < 1 ряд сходится, при I > 1 - расходится (при I = 1 вопрос
о сходимости ряда остается нерешенным).
Пример 5.3. Пользуясь необходимым признаком сходимости, показать, что ряд
расходится.
lim an = lim ——— = 1.
— —¥ n——¥ n +1
Таким образом, предел общего члена ряда при n — да отличен от нуля, т. е. необходимый признак сходимости не выполняется. Это означает, что данный ряд расходится.
Пример 5.4. Исследовать на сходимость ряд

111 1
--+--2 +--3 + ••• +---+ ••• •
5 • 2 5 • 2 5 • 2 5 • 2n
Решение. Сравним данный ряд с рядом

1 1 1 1
— +—2 +—3 + ••• +---+ ••• • (*)
2 22 23 2n
Ряд (*) сходится, так как его члены образуют бесконечно убывающую геометрическую прогрессию со знаменателем q =1 • При этом 1
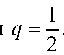

каждый член an =- данного ряда меньше соответствующего
5 • 2

члена bn = -1 ряда (*)• Поэтому, согласно признаку сравнения, данный ряд сходится •
Пример 5.5. Исследовать на сходимость ряд

1 1 1 1 +—j= +—т= + ••• +—т= + ••• •
Решение. Сравним данный ряд с гармоническим рядом

1 1 1
1 + —+ —+ ••• ^ —+ ••• •

Каждый член an = —^ данного ряда, начиная со второго, боль-

ше соответствующего члена bn =— гармонического ряда. Так как
n
гармонический ряд расходится, то, согласно признаку сравнения, расходится и данный ряд.
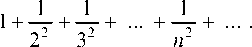
Решение. Каждый член ряда
(*)

меньше соответствующего члена ряда
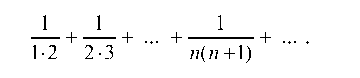
Как было показано в задаче 5.2, последний ряд сходится. Следовательно, сходится и ряд (*). Сходимость исходного ряда, отличающегося от ряда (*) наличием первого члена 1, теперь очевидна.
Пример 5.7. С помощью признака Даламбера решить вопрос
о сходимости ряда
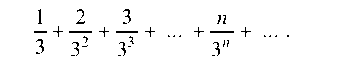
Решение. Для того чтобы воспользоваться признаком Даламбера, надо знать (п + 1)-й член ряда. Он получается путем подста-
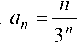
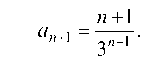
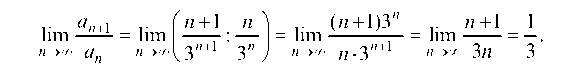

Пример 5.8. Пользуясь признаком Даламбера, исследовать на сходимость ряд

Решение. Знаянайдем (п + 1)-й член ряда
Вычислим
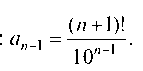
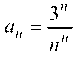

Пример 5.9. На основании признака Даламбера исследовать сходимость ряда
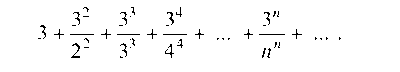
Решение. Зная n-й член ряда запишем (п + 1)-й член:
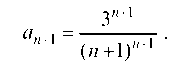
Отсюда
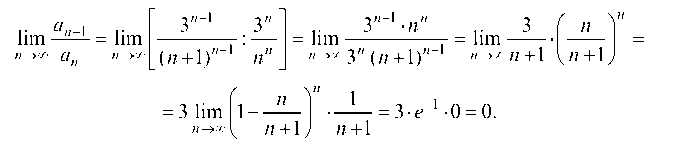
Так как I = 0 < 1, то ряд сходится.
| < Предыдущая | Следующая > |
|---|