4.4. Линейные уравнения
Уравнение вида
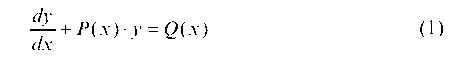

называется линейным уравнением.
Линейное уравнение сводится к двум уравнениям с разделяющимися переменными заменой искомой функции у произведением двух вспомогательных функций и и и, т. е. у = uu.
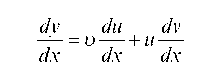
и уравнение (1) принимает вид

Пользуясь тем, что одно из вспомогательных переменных, например и, выбрано произвольно, подберем его так, чтобы выражение в квадратных скобках обратилось в нуль, т. е. в качестве и возьмем одно из частных решений u = v(x) уравнения с разделяющимися переменными

Подставив выражение u = v(x) в уравнение (2), получим уравнение относительно функции u:

Это также уравнение с разделяющимися переменными. Найдя общее решение этого уравнения u = u(x, C), получим общее решение уравнения (1):
Пример 4.9. Найти общее решение уравнения
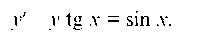
Решение. Положим у = uv, тогда у' = u'u + uV и данное уравнение принимает вид

или

Решая уравнение V - u tg x = 0, получим простейшее частное решение: 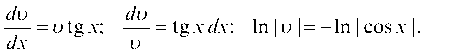

откуда

из которого находим и:

откуда
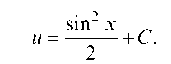
Пример 4.10. Решить дифференциальное уравнение:

Решение. Полагая у = и и, приводим это уравнение к виду

Приравняем квадратную скобку к нулю:  мы получим, что
мы получим, что

Подставляя полученное значение и в уравнение, получаем следующее уравнение для и:
Отсюда находим:

Таким образом,
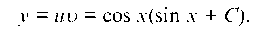
Итак, искомое общее решение

192
Пример 4.11. Рассмотрим следующую задачу:
Материальная точка движется по прямой линии в сопротивляющейся среде под действием периодически меняющейся силы = A sin at. Сопротивление среды пропорционально скорости движения. Вывести закон изменения скорости тела, если его начальная скорость равнялась нулю.
По условию на тело действуют две силы: сила сопротивления среды = - ku и периодическая сила F = A sin at. Общая сила равна F = - ku + A sin at. Но по второму закону Ньютона имеем F = ma, а ускорение — это производная скорости по времени:
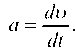 Отсюда приходим к уравнению
Отсюда приходим к уравнению
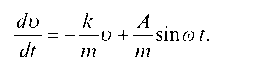
Это линейное уравнение первого порядка. Полагая и = м^, находим, что
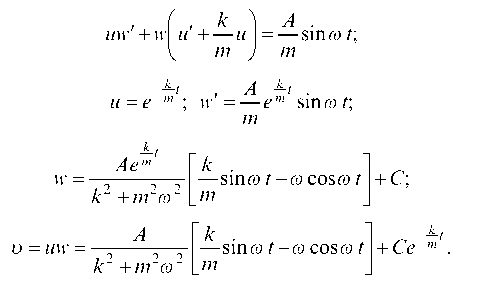
Полагая t = 0, u = 0, находим

имеем

| < Предыдущая | Следующая > |
|---|