4.3. Однородные уравнения

называется однородным уравнением.
Однородное уравнение приводится к уравнению с разделяющимися переменными подстановкой у = ux, где и — новая искомая функция.
Дифференцируя равенство у = ux, получим:


Подставив выражения у и в уравнение (1), имеем:

откуда
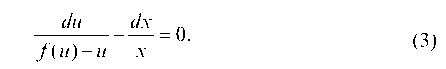
Это уравнение с разделяющимися переменными. Найдя общее решение (интеграл) уравнения (3), получаем общее решение (ин-
у
теграл) данного уравнения (1), заменив и на ^•
Пример 4.7. Найти общий интеграл уравнения 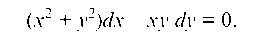
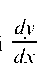
Решение. Разрешим уравнение относительно производной :
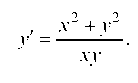
Поделив числитель и знаменатель правой части уравнения на х2, получим:

т. е. у' есть функция отношения Это означает, что данное уравнение — однородное.
Это означает, что данное уравнение — однородное.
Для решения этого уравнения введем новую функцию
Тогда у = ux и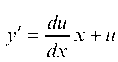 .Уравнение (*) преобразуется в урав
.Уравнение (*) преобразуется в урав
нение с разделяющимися переменными: 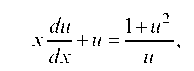
или

откуда

Интегрируя это уравнение, получим 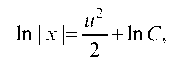 откуда
откуда 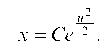
 т. е.
т. е.
Заменяя в последнем равенстве и отношением —, окончатель-
x
но получим:

dy x2 + у2
dx 2 xy
Решение. Делая подстановку у = хи, приводим уравнение к виду:
du 1 + и
x--+ и =-
dx 2и
Отсюда
du 1 + и 1 — и x— =--и = -
dx 2и
2и
и потому
dx 2udu. . . . .. 2 I, I _I
— =--; In | x |= — In 11 — и2 | +In | C |;
x 1 — и2
C
2
1—и
Cx 2 2 1 = ~2-г; x — у = Cx;
x2 — у2
2 = x2 — Cx; у = Wx2 — Cx.
у
Задача.
В теории резания возникает следующая задача: найти кривую, касательная к которой в каждой точке образует постоянный угол а с радиусом-вектором этой точки (рис. 52). По условию задачи имеем j = a + у и потому
tg j = tg(a +у) =
tga + tgy 1-tgatgy
(1)

Но из рис. 52 видно, что а, как известно, tg j = у'.
Поэтому равенство (1) можно записать так:

где для краткости положено k = tg а. Это — однородное уравнение. Сделаем подстановку у = xu. После простых преобразований получаем, что
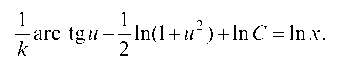

откуда находим
Подставляя вместо и значение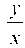 Получаем равенство:
Получаем равенство:
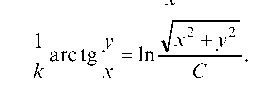
Это равенство проще записать в полярных координатах, положив.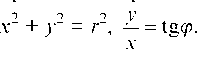 Мы получим, что
Мы получим, что
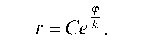
Эта кривая называется логарифмической спиралью.
| < Предыдущая | Следующая > |
|---|