4.2. Уравнения с разделяющимися переменными

Дифференциальное уравнение с разделяющимися переменными имеет вид:

Решается оно следующим образом. Поделив все члены уравнения на N1^) M2(x), получим уравнение

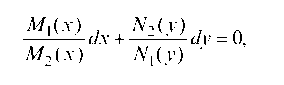
в котором переменные разделены. Общий интеграл уравнения находится почленным интегрированием:

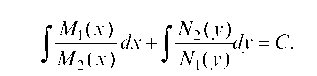
Пример 4.3. Найти общий интеграл уравнения

Решение. Разделим переменные в данном уравнении, поделив обе его части на выражение cos2 у ¦ sin2 x:

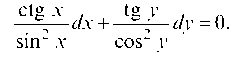
Интегрируя обе части данного уравнения, получим откуда

Воспользуемся тем, что С — произвольная постоянная и заменим С на. Тогда

Это и есть общий интеграл данного уравнения.

Пример 4.4. Найти общее решение дифференциального уравнения первого порядка

Решение. Выразим производную у' из уравнения.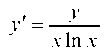

Правая часть разлагается на множители

следовательно, это уравнение с разделяющимися переменными. Разделим ихТеперь проинтегрируем обе части и для удобства допишем постоянную интегрирования в виде In с.

или

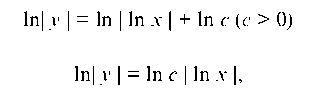
тогда

Окончательно у = с ¦ In x, где с — любое число. Итак, искомое общее решение у = с In x.

Пример 4.5. Найти частное решение уравнения (1 + е*)уу' = ex, удовлетворяющее начальному условию у |x = 0 = 1.

Решение. Имеем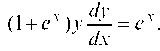Разделяя переменные, полу

чим:

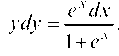
. Интегрируя, найдем общий интеграл:

Теперь найдем С. Положим х = 0, у = 1, тогда

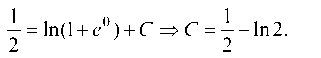
Подставляя значение С в выражение общего интеграла, найдем частный интеграл: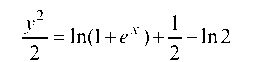

или

откуда

Из начального условия следует, что у > 0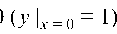, поэтому

перед корнем берем знак плюс. Итак, искомое частное решение:

Пример 4.6. Найти частный интеграл уравнения

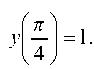
удовлетворяющий начальным условиям

Решение. Найдем общий интеграл данного уравнения. Для этого разделим переменные:

или

Интегрируя, получаем

Это и есть общий интеграл данного уравнения. Используя начальные условияПодставляем в выражение общего интеграла заданные значения переменных— тем самым определяем значение произвольной постоянной С:

откуда С = -1. Итак, искомый частный интеграл

< Предыдущая		Следующая >