4.0. Дифференциальные уравнения 4.1. Основные понятия
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ 4.1. Основные понятия
Уравнение, связывающее независимую переменную, неизвестную функцию и ее производные или дифференциалы различных порядков, называется дифференциальным уравнением.
Порядком дифференциального уравнения называется порядок старшей производной, входящей в это уравнение. Например, уравнение y' sin x + y tg x = 1 — первого порядка;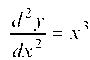 — второго
— второго
порядка; y'" - 5ху' + ху = 0 — третьего порядка.
Функция y = р (x), удовлетворяющая дифференциальному уравнению, называется решением этого уравнения. График решения называется интегральной кривой уравнения.
Если функция, удовлетворяющая дифференциальному уравнению, задана неявно, т. е. соотношением вида р (x, у) = 0, то говорят об интеграле уравнения.
Решение дифференциального уравнения, содержащее столько независимых произвольных постоянных, каков порядок уравнения, называется общим решением этого уравнения. Так, для уравнения первого порядка общее решение имеет вид:
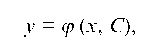
а для уравнения второго порядка — вид:
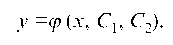
Функции, получаемые из общего решения при различных числовых значениях произвольных постоянных, называются частными решениями этого уравнения.
Геометрически общее решение определяет семейство кривых, а частное решение — некоторую кривую этого семейства.
Для нахождения частного решения дифференциального уравнения задаются начальные условия. Для уравнения первого по-
рядка они имеют вид у^0) = у0; для уравнения второго порядка — вид у^0) = у0, у'^0) = у'0. По этим начальным условиям определяются значения произвольных постоянных в общем решении уравнения, в результате чего получаются частные решения, удовлетворяющие заданным начальным условиям.
Пример 4.1. Проверить, что функция у = cos x является решением уравнения у" + у = 0.
Решение. Имеем
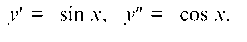
Подставляя выражения для у" и у в данное уравнение, получаем: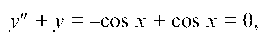
т. е., действительно, функция у = cos x является решением данного дифференциального уравнения.
Пример 4.2. Показать, что функция у, определяемая уравнением x2 - у2 = 4, является интегралом дифференциального уравнения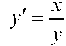 .
.
Решение. Продифференцировав обе части равенства по переменной x, получим:
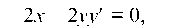
откуда
| < Предыдущая | Следующая > |
|---|