3.5. Приближенное решение алгебраических уравнений
3.5.1. Отделить положительный корень уравнения 4х - cos 2х = 0 и решить его приближенно с точностью s = 0,01:
а) методом деления отрезка попалам;
б) методом Ньютона (метод касательных).
Примечание. Можно считать, что точность s достигнута, если разность между соседними приближениями xk + i и хк удовлетворяет неравенству | хк + 1 - хк | < s.
а) Пусть дано уравнение
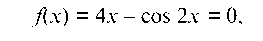
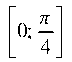
Р
где функция f(х) непрерывна на 0; — (функция f(х) изменяется
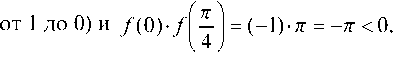
пополам и выбираем ту из половин
Делим


или
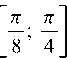
, на концах которой функция f(x) имеет противоположные
знаки и, так как, то выбираем

и т. д.

Последовательно имеем:
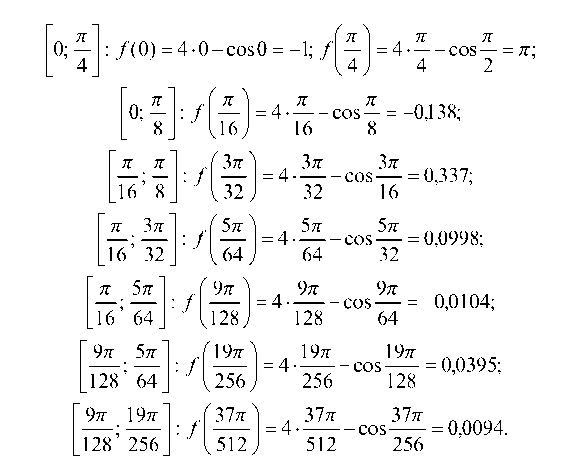
Так как
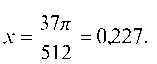
б) Отделяем положительный корень уравнения


то можно принять
методом Ньютона.
Учитывая предыдущее решение, заключаем, что искомый ко-
рень находится на
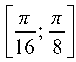
, имеем:
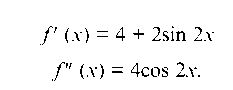
pp

Отсюда f (х) > 0 и f " (х) > 0 при — < х < —. Так как должно
16 8
быть f (х0) ¦ f" (х0) > 0, то за начальное приближение принимаем х0 =Р, ибо flpj = 4 •pp - cos Р = 0,864 > 0. Вычисление произво-

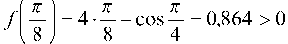
дим по следующей схеме:
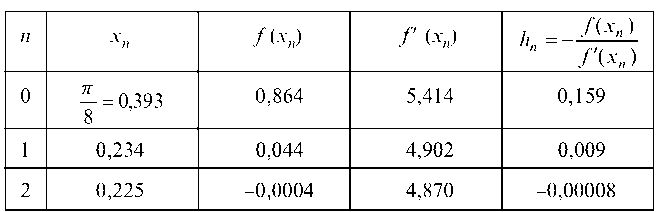
Находим f'(х0) = f = 4 + 2sin0,786 = 5,414, затем h0. Вычисляем
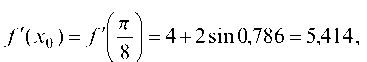
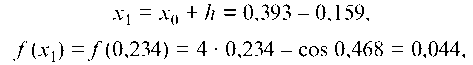
х1 = х0 + h = 0,393 - 0,159,
f (х1) = f (0,234) = 4 ¦ 0,234 - cos 0,468 = 0,044,
затем Д'(х1) и h1. Далее определяем
х2 = х1 + h = 0,225,
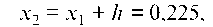
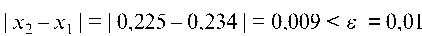
f (х2) и f' (х2). Так как | х2 - х1 | = | 0,225 - 0,234 | = 0,009 < s = 0,01, то за положительный корень принимаем 0,225.
| < Предыдущая | Следующая > |
|---|