3.4. Приложения производной
3.4.1. Составить уравнения касательных к кривой у = 3х + 2
параллельных прямой 3х + у + 3 = 0.
Решение. Пусть М (х0; у0) — координаты точки касания касательной и кривой. Уравнение касательной выбираем в виде:
у - у0 = ¦ (х - х0).
Так как касательная параллельна прямой 3х + у + 3 = 0, угловой коэффициент которой к„р, = -3, то kkac. = = -3.
Найдем производную:
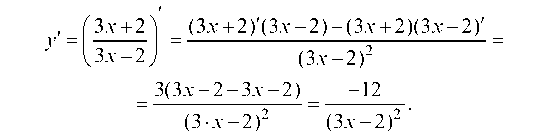
Так как производная у в точке касания (x0; у0) численно равна угловому коэффициенту касательной, то
отсюда
Получаем
тогда
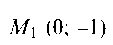
Имеем две точки касания и соответственно
которым запишем два уравнения касательных: у + 1 = -3(х - 0), отсюда
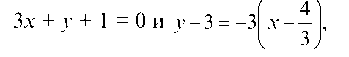
отсюда
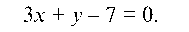
3.4.2. Найти наибольшее и наименьшее значения функции f (x) = 2x3 + 3x2 - 36x + 1 на отрезке [1; 11].
Решение. Данная функция непрерывна на [1; 11]. Находим f '(x) = 6x2 + 6x - 36 = 0. Полагая у' = 0, имеем x2 + x - 6 = 0,
отсюда получаем две критические точки: x1 = -3 и x2 = 2. Для нахождения наименьшего и наибольшего значений функции на заданном отрезке достаточно вычислить ее значения на концах отрезка и в точке х = 2, так как точка х = -3 не принадлежит отрезку [1; 11]. Получим: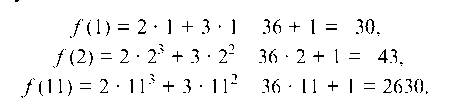
Следовательно, наименьшее значение функции равное (-43), достигается в критической точке х = 2, а наибольшее равно 2630 — на правом конце отрезка, в точке х = 11.
3.4.3. Исследовать методами дифференциального исчисления и построить график функции:
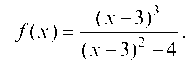
1. Область определения функции.
Область определения — вся ось Ох за исключением точек х = 5 и х = 1.
2. Точки разрыва и интервалы непрерывности.
Точки разрыва х = 5 и х = 1. Интервалы непрерывности (-¥; 1), (1; 5), (5; ¥).
3. Слева от точек разрыва х = 1 и х = 5 функция f (x) ® -¥, а справа — f (x) ® +¥.
Вертикальные асимптоты: x = 1 и x = 5.
4. Точки пересечения с осями координат. С осью Ох : у = 0, тогда
, отсюда x = 3.
С п 0 /( ) (0 - 3)3 27
С осью Оу : х = 0, тогда f (х) = —-^— =--.
(0 - 3)2 - 4 5
( 27 ^
Получим точки: I 0; - — I и (3; 0).
5. Симметрия графика.
И V, „ч (-4 - 3)3 343
(4 - 3)3 =_ 1 (4 - 3)2 - 4 = 3.
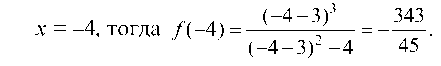
х = -4, тогда f (-4) = —-^— =--.
(-4 - 3)2 - 4 45
Так как f(4) ф f(-4), то функция общего вида.
6. Находим производную
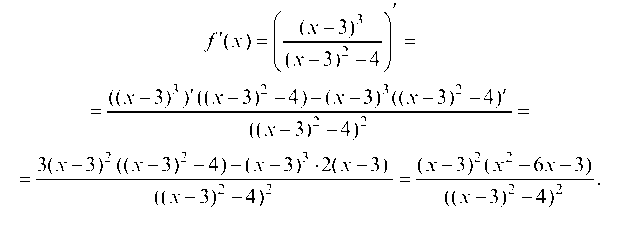
= 3(х - 3)2 ((х - 3)2 - 4) - (х - 3)3 • 2(х - 3) = (х - 3)2(х2 - 6х - 3)
= ((х - 3)2 -4)2 = ((х - 3)2 - 4)2 .
Находим критические точки:
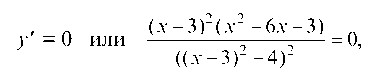
х1 = 3 - 273, х2 = 3 + 2л/3, х3 = 3.
' = 0 (х-3)2(х2 -6х-3) 0 у' = 0 или ----—- = 0,
((х - 3)2 - 4)2
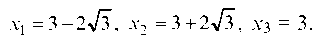
отсюда
Исследуем знаки у' при переходе через критические точки.
В интервалах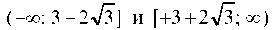
Функция возрастает,
в интервале
Функция убывает.
Так как при переходе через точку
Производная ме
няет знак с «+» на «-», то это точка max. Точка
Будет
точкой min, так как при переходе через нее производная меняет знак с «-» на «+». Найдем:
7. Для отыскания интервалов выпуклости и вогнутости и точек перегиба найдем вторую производную:
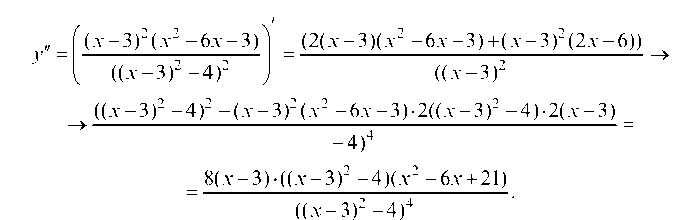
Из условия у" = 0 имеем х - 3 = 0 или х = 3. Условию у" = ¥ соответствует х = 1 и х = 5 (точки разрыва функции). Наносим эти три точки на числовую ось и исследуем знак второй производной на каждом из интервалов:
В интервалах (-да; 1) и [3; 5) график функции — выпуклый, а в интервалах (1; 3] и (5; да) — вогнутый. В точке х = 3 график функции меняет направление выпуклости и так как /(3) = 0, то точка (3; 0) есть точка перегиба.
8. Наклонную асимптоту ищем в виде:
где
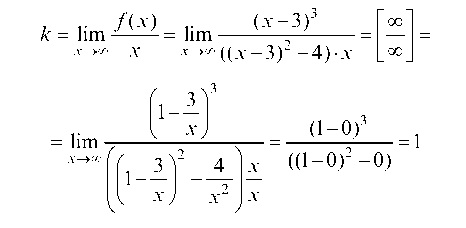
и
Следовательно, наклонная асимптота имеет вид: у = х - 3.
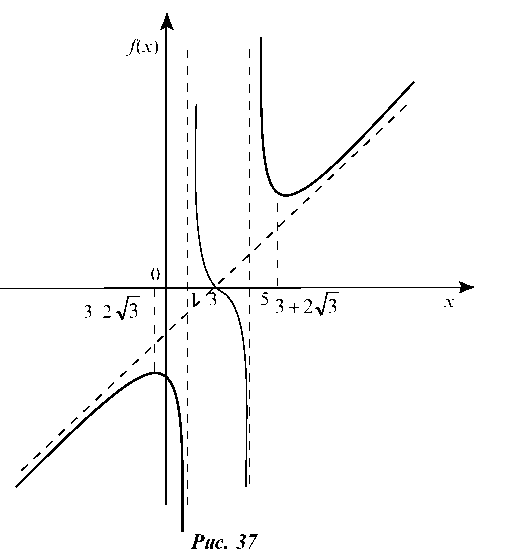
9. Строим график функции (рис. 37).
Замечание. Вводя новую переменную t = x - 3, можно рас-
сматривать функцию
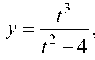
исследовать и построить ее гра-
фик, а затем перенести ось 0/(x) на 3 ед. влево и вместо оси Ot написать ось Ox.
| < Предыдущая | Следующая > |
|---|
