3.3. Производные функции
3.3.1. Найти производные у '(х) функций:

При нахождении производной у' применим теоремы о производной сложной функции, о производной степенной функции,
о производной от алгебраической суммы функций, о выносе постоянной величины за знак производной: (с ¦ f(х))' = с ¦ f' (х) и о производной от постоянной величины: (с)' = 0:

в) у = 1п 4

. Используя свойства логарифмов, имеем:

б) у = 3х. Применяя теоремы о производной от сложной функции и о производной от показательной функции, получим:

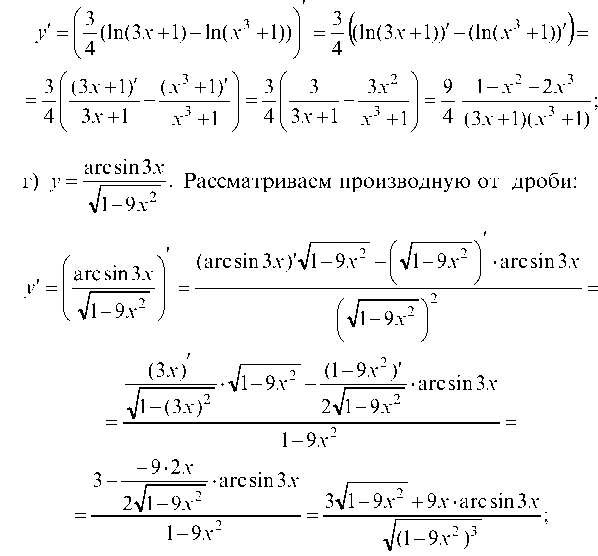

д) y = (2x)sin3x. Здесь основание и показатель степени зависят от х. Логарифмируя, получим:
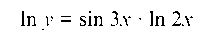
ln y = sin 3x • ln 2x
Дифференцируем обе части последнего равенства по х. Так как
(ln у) ' = (sin3x • ln2 x)' , У = (sin3x) ' • ln2 x + sin3x • (ln2 x) ' ,
У 14
у является функцией х, то ln у есть сложная функция х и (ln у) ' = Следовательно,
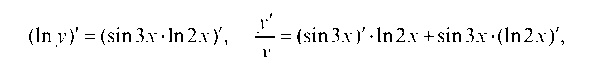
У

и окончательно
у ' = (2x )sin3x ^3cos3x • ln2x +1 sin3xj;
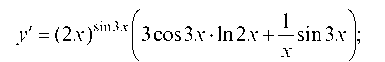
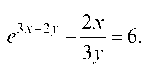
2x
e) e3x+2y--= 6. Функция задана неявно. Для того, чтобы най-
3У
ти у' , продифференцируем обе части равенства по х, считая у функцией от х, а затем разрешим уравнение относительно у' :
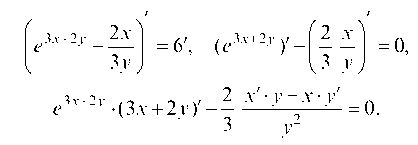
Приводим к общему знаменателю:
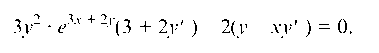
3у2 • e3x + 2y(3 + 2у' ) - 2(y - xy' ) = 0.
Отсюда находим
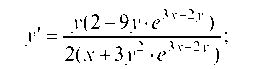
y'= y(2 - 9y • e3x+2y) ’
) (у = 1п4? + 2? + 4,

Ж) [х = 2?2 + 2? + 8.
Здесь функция у аргумента х задана параметрическими уравнениями и тогда:

| < Предыдущая | Следующая > |
|---|