3.3. Функции нескольких переменных
Пример 3.20. Найти область существования функции

Решение. Решив систему уравнений
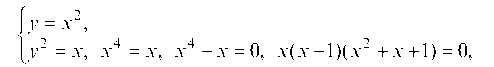
2
Решение. Функция имеет действительные значения, если 4 - x -2 2 2
- у > 0 или x + у < 4. Последнему неравенству удовлетворяют
координаты точек, лежащих внутри окружности радиуса 2 с цен-168
тром в начале координат. Область существования функции есть множество точек внутри этого круга (рис. 44).

Рис. 44
Пример 3.21. Найти точки разрыва функции
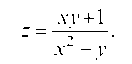
Решение. Функция потеряет смысл, если знаменатель обратится в нуль. Но x2 - у = 0 или у = x2 — уравнение параболы. Следовательно, данная функция имеет линией разрыва параболу у = x2.
Пример 3.22. Найти частные производные функции z = / (x; у):
a) z = / (x; у) = x5 - 2xy2 + 3xy - x.
Рассматривая y как постоянную величину, получим
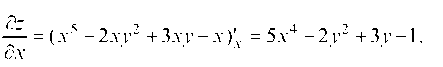
Полагая теперь х постоянной величиной, получим

б) z = ln(x3 + y3).
Рассматривая у как постоянную величину, получим 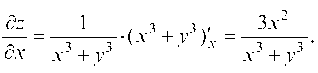
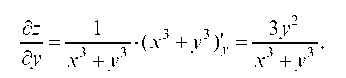
Полный дифференциал функции z = f (x; у) определяется формулой

Пример 3.23. Найти полный дифференциал функции 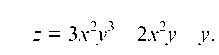 Находим прежде всего частные производные
Находим прежде всего частные производные

Тогда полный дифференциал равен 
Пример 3.24. Найти частные производные второго порядка жции z = cosx5y2.
Сначала находим частные производные первого порядка.

Тогда 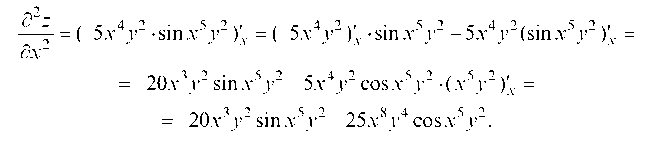
Производной функции z = /(x, у) в данном направлении а называется:
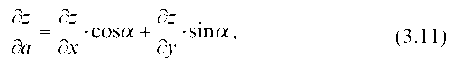
где а — угол, образованный вектором а с осью Ox.
Градиентом функции z = /(x, у) называется вектор, проекциями которого на координатные оси являются соответствующие частные производные данной функции:
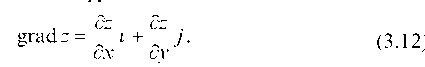 )
)
Производная данной функции в направлении а связана с градиентом функции следующей формулой:

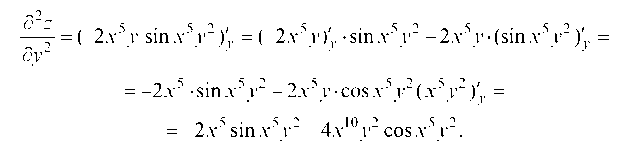
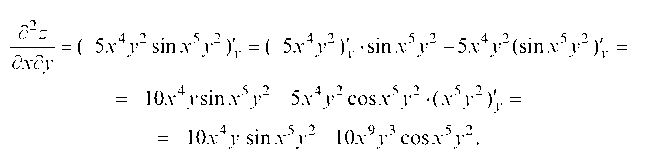
Пример 3.25. Найти градиент функции z = x2 - xy + у3 в точке А(1;-1) и производную по направлению вектора a = 3i - 4 j. Решение. Частные производные равны: 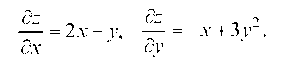
По формуле (3.12):
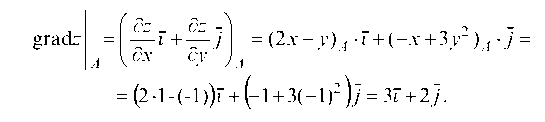
(необходимые условия экстремума).
Достаточные условия существования экстремума функции двух переменных заключаются в следующем: пусть f'x (a; b) = fy (a; b) = 0 и A = fxx (a; b), B = f (a; b), C = f'yy (a; b). Составим дискриминант

Тогда: 1) если Д > 0, то функция имеет экстремум в точке P(a; b), а именно, максимум, если A < 0 (или С < 0), и минимум, если А > 0 (или С > 0); 2) если Д < 0, то экстремума в точке P нет;
3) если Д = 0, то вопрос о наличии экстремума в точке P остается открытым (требуется дальнейшее исследование).
Пример 3.26. Найти экстремумы функции


Используя частные производные, можно решать задачи на отыскание экстремума функции нескольких переменных.
Точки, в которых дифференцируемая функция f(x; y) может достигать экстремума (так называемые стационарные точки), находятся путем решения системы уравнений
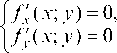
Решение. Определим стационарные точки z, решая систему

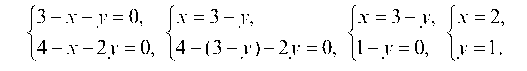
Таким образом, z имеет две стационарные точки: А (4; 0) и B (2; 1).

или, если
Используем достаточные условия экстремума. Для этого найдем частные производные z второго порядка.
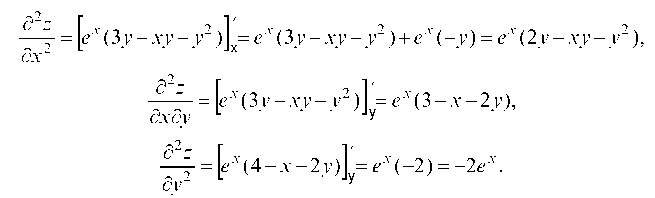
Тогда
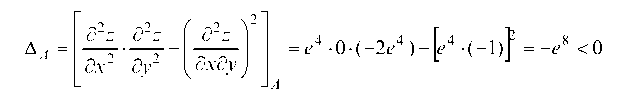
и в точке A нет экстремума.
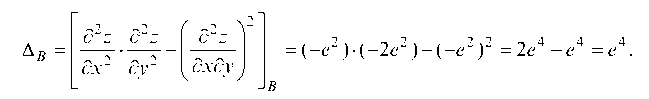
Так как имеет максимум.
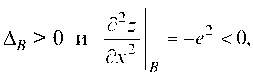
то в точке В функция z
Таким образом функция z = ex (4y - xy - y ) имеет единственный экстремум — максимум в точке В (2; 1).
| < Предыдущая | Следующая > |
|---|