3.2.3. Приложения определенного интеграла
Геометрический смысл определенного интеграла (3.4) состоит в том, что если график функции y = f (x) ограничивает криволинейную трапецию Ф = {(x, y) | a < x < b, 0 < y <f (x)}, то его величина равна площади этой трапеции. Чтобы убедиться в этом, доста-
точно рассмотреть рис. 38 и заметить, что площадь криволинейной трапеции:


Это равенство тем точнее, чем больше n. Поэтому точное значение:
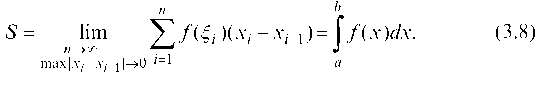
Объем тела, образованного вращением криволинейной трапеции вокруг оси Ох, вычисляется по формуле:

а длина дуги линии y = /(x), заключенной между точками с абсциссами а и b, вычисляется по формуле:

Пример 3.14. Вычислить площадь фигуры, ограниченной линиями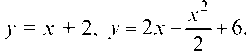 Сделать чертеж.
Сделать чертеж.
Находим точки пересечения заданных линий. Для этого решаем систему уравнений:
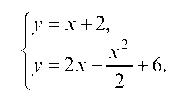
Для нахождения абсцисс точек пересечения заданных линий решаем уравнение:

Находим: х1 = -2, х2 = 4.
Итак, данные линии, представляющие собой параболу и прямую, пересекаются в точках А(-2; 0), В(4; 6) (рис. 39).
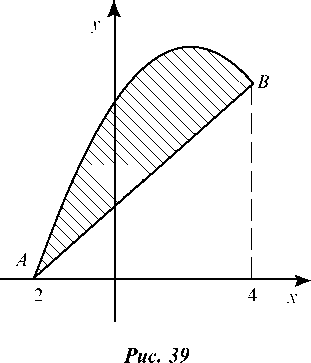
Эти линии образуют замкнутую фигуру, площадь которой вычисляем по указанной выше формуле:
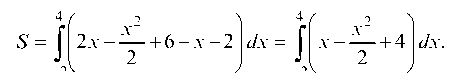

Пример 3.15. Вычислить площадь фигуры, ограниченной линиями у = - х2 + х + 4 и у = - х + 1.
Найдем точки пересечения линий у = - х2 + х + 4, у = - х + 1, приравнивая ординаты линий: - х2 + х + 4 = - х + 1 или х2 - 2х - 3 = 0. Находим корни х1 = -1, х2 = 3 и соответствующие им ординаты у1 = 2, у2 = -2 (рис. 40).

По формуле площади фигуры получим:
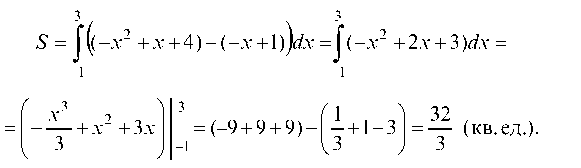
3 3
£ = Л-х2 + х + 4) - (-х +1)]^х = Л-х2 + 2х + 3}^х :
Пример 3.16. Найти площадь, заключенную внутри лемнискаты Бернулли r2 = a2 cos 2 j (рис. 41).

Рис. 41
В полярной системе координат площадь фигуры, ограниченной дугой кривой r = f(j) и двумя полярными радиусами j = а и j2 = b, выразится интегралом

В силу симметрии кривой (рис. 41) определяем сначала одну четвертую искомой площади:

Отсюда S = a.

Пример 3.17. Найти длину астроиды (рис. 42).
Дифференцируя уравнение астроиды, получим: 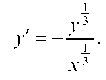
Отсюда L = 6a.
Пример 3.18. Вычислить объем тела, образованного вращением фигуры, ограниченной одной полуволной синусоиды y = sin x вокруг оси Ох.
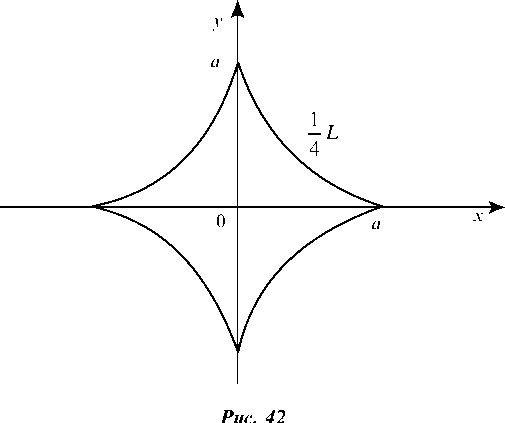
Поэтому для длины дуги одной четверти астроиды имеем:


Пример 3.19. Вычислить объем тела, полученного вращением вокруг оси Ох фигуры, ограниченной параболами y = x2 и х = j2 (рис. 43).

Рис. 43
получим x1 = 0, x2 = 1, y1 = 0, y2 = 1, откуда точки пересечения кривых 0(0; 0), В(1; 1). Как видно (рис. 43), искомый объем тела вращения равен разности двух объемов, образованных вращением вокруг оси Ox криволинейных трапеций OCBA и ODBA:
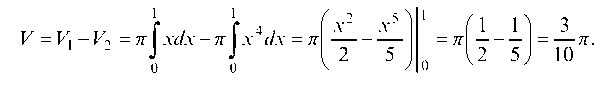
| < Предыдущая | Следующая > |
|---|