3.2.2. Вычисление определенного интеграла

Определенный интеграл связан с неопределенным интегралом по формуле:

где F(x) — произвольная первообразная функция / (x).

Формула (3.5) называется формулой Ньютона-Лейбница.

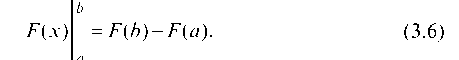
Замена переменной в определенном интеграле отличается от замены переменной в неопределенном интеграле тем, что:

1) необходимо изменить пределы интегрирования;

2) возвращаться к первоначальной переменной не надо.

Пример 3.13. Пользуясь формулой Ньютона-Лейбница, вычислить определенный интеграл

Решение. Чтобы избавиться от иррациональности, сделаем

2

подстановку 1 + х = t. Тогда

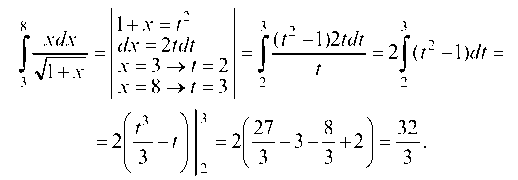
Формула интегрирования по частям в определенном интеграле:

вычисляется по формуле (3.6).

, (3.7)

где

< Предыдущая		Следующая >