3.2.1. Пределы, непрерывность и разрывы функций
3.2.1. Найти пределы функций:
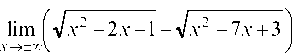
а)
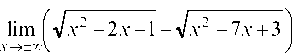 (неопределенность бесконечность-бесконечность).
(неопределенность бесконечность-бесконечность).
Решение. Умножим и разделим рассматриваемое выражение x2 -2x-1 +Vx2 -7x + 3j:
на

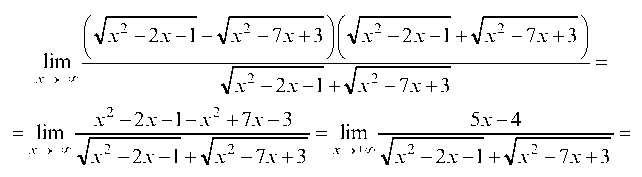
при этом перед lim ставим знак «±»)


• 22 - 20 • 2 + 8 0
=--неопределенность

±¥
(неопределенность —; числитель и знаменатель разделим на х и
¥
х®2>/4х-4 2х + 4 [ТЇЗ - V 2 • 2 + 4 0
Многочлен в числителе раскладываем на множители и числитель и знаменатель умножим на (/4х +42х + 4):

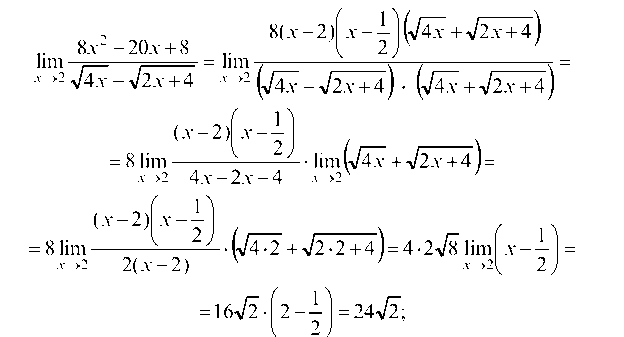
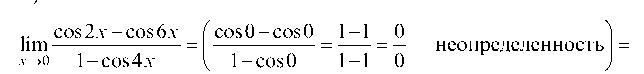
(в числителе применяем формулу преобразования суммы в произведение, а в знаменателе — формулу половинного аргумента)
.. cos2x - cos6x (cos0 - cos0 1 -1 0 ]
lim-_ I-_-_--неопределенность I _
x®0 1-cos4x - 1 - cos0 1 -1 0 )
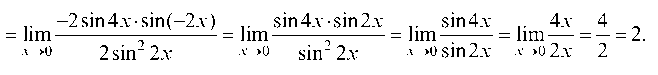
Заменили числитель и знаменатель дроби эквивалентными бесконечно малыми: sin 4x ~ 4x; sin 2x ~ 2x;
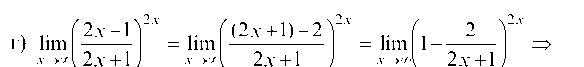
Обозначим теперьоткуда, причем при
х — ¥ имеем а — 0.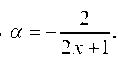

Тогда
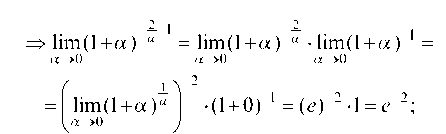
д)
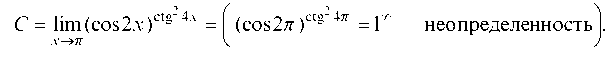
Полагаем cos 2х = 1 + а(х), где lim а(х) = 0 и следовательно,
х——П
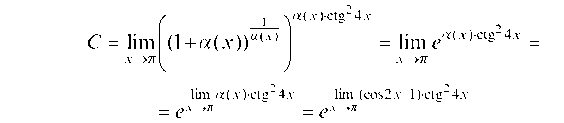
Вычисляем:
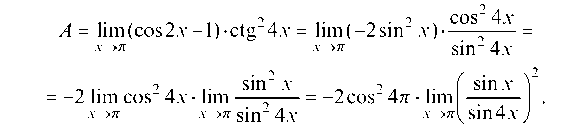
Пусть t = х - п, отсюда х = п + t и, если х — p то t — 0. Тогда

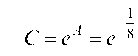

окончательно lim(cos2x)ctg 4x = e 8.
x——P
Положили ß = 4t и, если t — 0, то ß — 4 ¦ 0 — 0. Имеем -1 2 1 C = eA = e 8 '
3.2.2. Определить характер точек разрыва или установить непрерывность функции f (х) в точках х1 = 0 и х2 = 2. Схематически изобразить поведение f (х) в окрестностях этих точек:
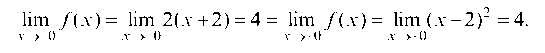
В точке х = 2 функция /(x) имеет разрыв 1-го рода, т. к. lim /(x) = lim (x-2)2 = (2 -0 -2)2 = 0 и lim /(x) = lim 4x =
X—2-0 x—2-0 x—2+0 x—2+0

б)
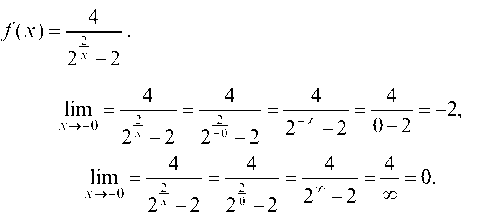
В точке х = 0 имеем разрыв 1-го рода.
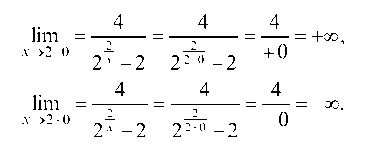
В точке х = 2 имеем разрыв 2-го рода.
Рассмотрим поведение функции на бесконечности

(см. рис. 36).
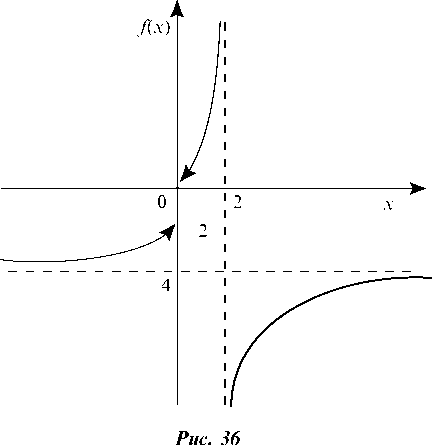
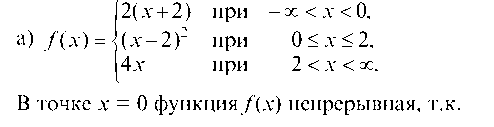
Lim /(x) = lim 2(x + 2) = 4 = lim /(x) = lim (x - 2) = 4.
X—-0 x—-0 x—+0 x—+0

| < Предыдущая | Следующая > |
|---|