3.2. Определенный интеграл

3.2.1. Основные понятия и свойства

Пусть y = f(x) — непрерывная на [a, b] функция. Разобьем [a, b] точками а = х0 < х1 < х2 < ... < xn _ 1 < xn = b на n частичных отрезков

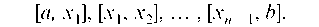
В каждом из них выберем по одной произвольной точке

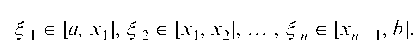
Итак, подинтегральное выражение преобразовано к дробнорациональному виду. Выделяем целую часть и разложим на простейшие дроби:

Отсюда

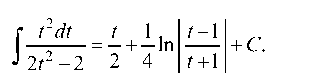
Возвращаясь к старой переменной x cos x = t, находим:

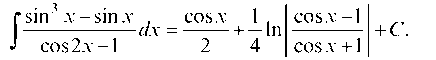
160

Определенным интегралом от функции /(x) по [a, b] называется величина

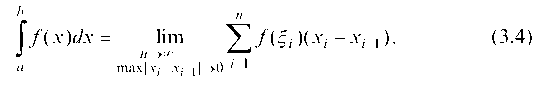
Свойства определенного интеграла:

:)dx.

< Предыдущая		Следующая >