3.1.5. Интегрирование дробно-рациональных функций
Дробно-рациональной функцией (рациональной дробью) называется отношение двух многочленов. Если степень многочлена, стоящего в числителе дроби, не меньше, чем степень многочлена в знаменателе, то в этой дроби следует выделить целую часть, т. е. представить ее в виде:
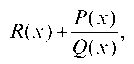
где R(x), P(x), Q(x) — многочлены, причем степень P(x) меньше степени Q(x). Рациональная дробь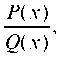
Обладающая этим свой
ством, называется правильной. Для интегрирования такой дроби ее необходимо разложить в сумму простейших дробей, которые легко интегрируются: казано ниже на примере). Остановимся подробнее на методике разложения правильной рациональной дроби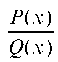
В сумму про
т. е. этот квадратный трехчлен не имеет действительных корней (интегрирование простейших дробей последнего типа будет по-
стейших дробей. Это выполняется по следующей схеме:
1. Сначала знаменатель дроби Q(x) необходимо разложить на множители вида: x - a, (x - b)k, (x2 + px + q)k.
При этом часто используется теорема Виета: если квадратный трехчлен ax2 + bx + с имеет корни X1, х2, то
2. Далее следует записать разложение дроби
В сумму простейших дробей, оставляя неопределенными коэффициентами А, B, C, D и т. д. При этом каждому множителю вида (x - а) соответствует дробь, множителю вида (x - b)k соответствует сумма дробей:
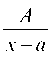
а множителю вида x2 + px + q, если он не имеет действительных корней (p2 - 4q < 0), соответствует дробь вида:
3. Для определения коэффициентов А, B, C, D, E в этом разложении следует приравнять коэффициенты при одинаковых степенях х у многочлена P(x) и многочлена, который получается в числителе после приведения записанной суммы простейших дробей к общему знаменателю (метод неопределенных коэффициентов). Можно также находить эти коэффициенты путем сравнения значений указанных многочленов при конкретных значениях х (в первую очередь, при х, совпадающих с корнями знаменателя Q(x)).
Пример 3.8. Вычислить интеграл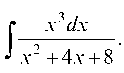
Подинтеграль-
ная функция представляет собой неправильную рациональную 156
дробь, поэтому выделим сначала целую часть дроби, поделив с остатком числитель на знаменатель
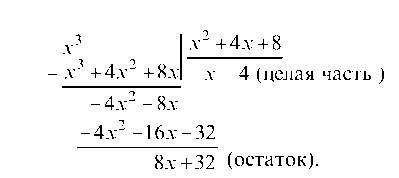
Таким образом
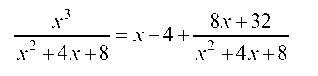
и
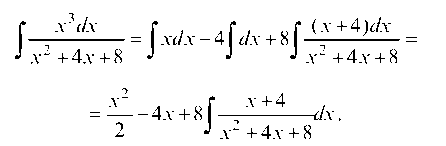
Для нахождения оставшегося интеграла выделим в числителе дифференциал знаменателя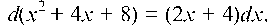
Затем разобьем интеграл на два слагаемых и в последнем выделим полный квадрат квадратного трехчлена, стоящего в знаменателе. Тем самым получим:
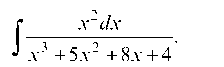
1. Подинтегральная функция — правильная рациональная дробь.
2. Разложим знаменатель правильной рациональной дроби на простейшие действительные множители:
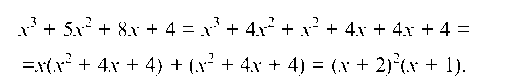
3. Разложим правильную рациональную дробь на простейшие:
Так как в знаменателе правильной дроби есть кратный линейный множитель, то в разложении появилась простейшая дробь
II типа.
4. Приведем к общему знаменателю все дроби и затем отбросим его:
Таким образом, имеем
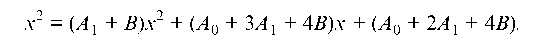
5. Составляем систему уравнений:
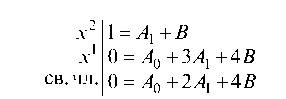
6. Решая систему уравнений, получим A0 = -4, A1 = 0 и В = 1, а исходная подинтегральная функция разложится на простейшие дроби следующим образом:
Пример 3.10. Найти интеграл
I">
Решение. Заметим, что
.
Наименьшим общим кратным знаменателем дробей
Является
6. Поэтому, если применить подстановку 2х + 3 = t6, то будет иметь:
т. е. иррациональности в подинтегральном выражении исчезают. Так как: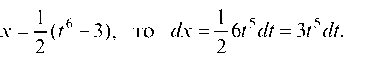
Подставляя найденные выражения в искомый интеграл, получаем:
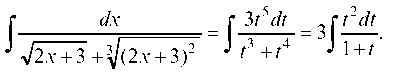
Таким образом, данный интеграл сведен к интегралу от рациональной функции. Для его нахождения выделим целую часть подинтегральной функции:
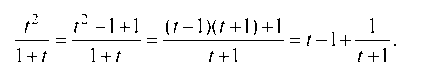
Интегрируя каждое из слагаемых, находим:
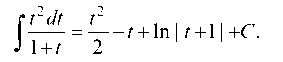
Возвратимся к старой переменной. Так как
То по
лучаем следующий окончательный результат:
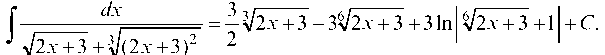
159
2
Так как cos 2x = 2cos x - 1, то подинтегральная функция имеет вид R(sin x, cos x). Заметим, что при замене sin x на - sin x она меняет знак, т. е. является нечетной относительно sin x. Применяем подстановку cos x = t. Тогда
| < Предыдущая | Следующая > |
|---|
