3.1.4. Метод интегрирования по частям
Применение этого метода основывается на формуле:
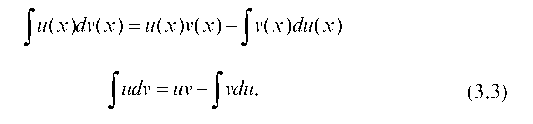
или
Ясно, что эту формулу имеет смысл применять лишь тогда, когда интеграл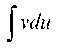
Оказывается более удобным для интегриро
вания (возможно даже, табличным), чем исходный интеграл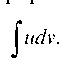
Возникает вопрос: как представить подходящим образом подин-тегральное выражение f (x)dx в виде u(x)dv(x). Общего правила для этого нет. Однако можно пользоваться следующими частными указаниями:
1. Если подинтегральное выражение содержит произведение показательной (еах) или тригонометрической функции (sin ax, cos ax) на многочлен, то за множитель u(x) следует принять многочлен.
2. Если подинтегральное выражение содержит произведение логарифмической (In ax) или обратной тригонометрической функции (arcsin ax, arccos ax и т. д.) на многочлен, то за множитель u(x) следует принять логарифмическую или обратную тригонометрическую функцию.
Пример 3.5.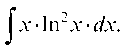
Применим формулу интегрирования
по частям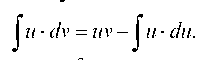
Положим
Тогда
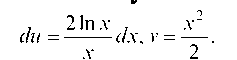
По формуле получим:
Снова применим формулу интегрирования по частям, положив u = In x, dv = xdx. Тогда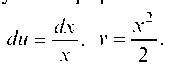
Тогда
2
Полагаем u = x. Оставшееся под интегралом выражение обозначаем через dv и преобразуем его с помощью приема «подведения функции под знак дифференциала»:
Для применения формулы интегрирования во частям вычислим du и v:
Согласно формуле интегрирования по частям, имеем:
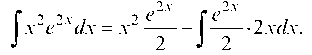
Итак, исходный интеграл свелся к вычислению интеграла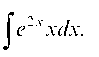 
К нему вновь применяем формулу интегрирования по частям:
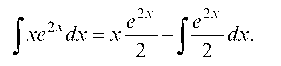
Итак, получили интеграл табличного вида:
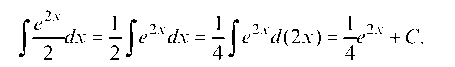
Суммируя проведенные вычисления, имеем окончательно:
Пример 3.7. Найти интеграл
Принимаем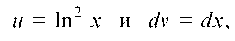
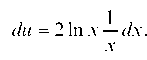Тогда
, а
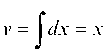И, применяя формулу (3.3), имеем:
154
dv = dx. Имея в виду, что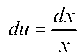
И v = x, используя второй раз
формулу (3.3.), получим:
>
а искомый интеграл будет иметь следующий вид:
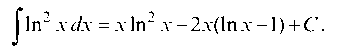
| < Предыдущая | Следующая > |
|---|
