3.1.3. Интегрирование методом замены переменной
Пусть требуется вычислить интеграл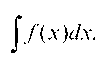
Не являющий
ся табличным. Введем вместо х новую переменную t, связанную с х зависимостью х = j(t), где j(t) — дифференцируемая функция, для которой существует обратная функция. Тогда dx = j(t)dt и будет иметь место формула:
(3.1)
Выражение (3.1) называют формулой замены переменной.
Существует другой способ замены переменной интегрирования.
Если под знаком интеграла стоит сложная функция, умноженная на производную, т. е.
То удобно сделать замену
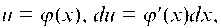И тогда будем иметь:
Отметим, что формулы (3.1) и (3.2) различаются только обозначениями переменных интегрирования.
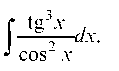
Пример 3.1. Вычислить интеграл
Сделаем замену переменной tg x = t, тогда
Получим табличный интеграл где С — произ
вольная постоянная. Производя обратную замену переменной, получим:
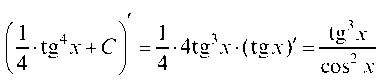
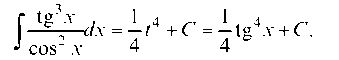
Проверка. — подинтег-
ральная функция.
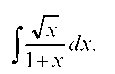
Пример 3.2. Найти интеграл
2
Введем новую переменную интегрирования
Тогда x = t
и dx = 2tdt. Используя формулу (3.1), будем иметь:
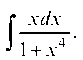
менную интегрирования u = x2. Тогда du = 2xdx, и данный интеграл будет иметь вид табличного:
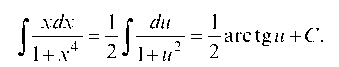
Возвращаясь к старой переменной интегрирования, имеем: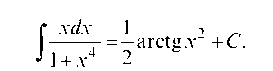 
Пример 3.4. Найти неопределенный интеграл
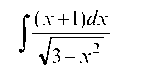
и проверить результат дифференцированием.
Решение. Данный интеграл разложим на сумму двух интегралов:
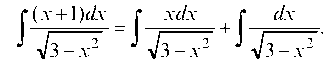
Для вычисления первого из этих интегралов воспользуемся тем, что
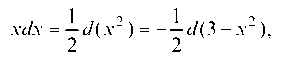
(и тем самым, множитель х «подведем под знак дифференциала»), и сделаем замену переменной:
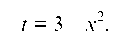
Получаем: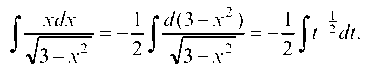 
Полученный интеграл является табличным: Применяя эту формулу при имеем:
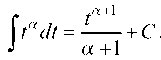
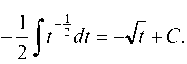
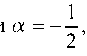
Аналогично вычисляем интеграл
Окончательно имеем:
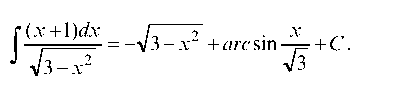
Проверка. Убедимся, что производная от полученного выражения совпадает с подинтегральной функцией. Применяя таблицу производных и правило дифференцирования сложных функций, находим:
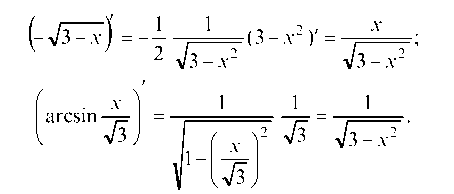
Складывая эти два выражения, получаем подинтегральную функцию. Следовательно, интегрирование выполнено правильно.
| < Предыдущая | Следующая > |
|---|
