3.1.2. Таблица основных интегралов

Рассмотрим свойства неопределенных интегралов.

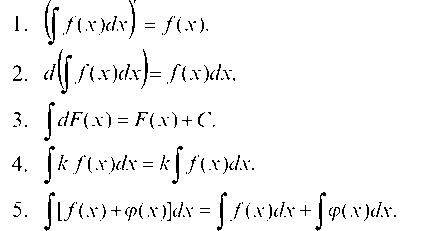
3. fdF(х) = F(х) + C.

4. Jf(х)dx = kff(х)dx.

5. f[f(x) + j(x)]dx = j" f (x)dx + j" j(x)dx.

В интегральном исчислении нет общего приема нахождения неопределенного интеграла. Существует несколько методов, которые дают возможность свести заданный интеграл к так называемому табличному. Прием, когда заданный интеграл можно сразу вычислить, используя его свойства и таблицу основных интегралов, называют непосредственным интегрированием.

Таблицы основных интегралов приведены в соответствующих разделах учебников, их необходимо выучить наизусть.

Необходимо обратить внимание на тесную связь этой таблицы с таблицей производных (задача нахождения неопределенного интеграла является обратной по отношению к задаче нахождения производной). Процесс интегрирования (нахождения неопределенного интеграла) по сравнению с дифференцированием (нахождением производной) может представлять значительные трудности. При дифференцировании задача сводится к тому, чтобы в таблице производных найти подходящую формулу, исходя из которой с помощью правил дифференцирования вычисляется искомая производная заданной функции. При интегрировании же нет какого-либо общего приема вычисления неопределенных интегралов. Имеется лишь ряд методов, позволяющих свести данный интеграл к табличным. Поэтому для каждого данного интеграла нужно суметь найти подходящий метод, с помощью которого преобразовать данный интеграл к табличному виду, а затем найти его по соответствующей формуле таблицы интегралов. Рассмотрим простейшие методы нахождения неопределенных интегралов.

< Предыдущая		Следующая >