3.1. Неопределенный интеграл. 3.1.1. Первообразная функция и неопределенный интеграл

3.1.1. Первообразная функция и неопределенный интеграл

В дифференциальном исчислении по заданной функции F(x) находят ее производную / (x) = F' (x). На практике часто приходится решать обратную задачу: требуется восстановить функцию F(x), зная ее производную / (x). Функцию F(x) в этом случае называют первообразной для / (x).

Определение 1. Функция F(x) называется первообразной для функции / (x), если производная F(x) равна / (x), т. е.

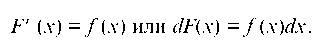
Пример. Пусть имеем функцию / (x) = 2х. Функция F(x) = x является первообразной для / (x), т. к. (x2)' = 2x. Но функция F(x) = x2 + 1 тоже является первообразной функции / (x), так как (x2 + 1)' = 2х, и вообще — любая функция F(x) = x2 + С (где С — произвольная постоянная) есть первообразная для / (x). Таким образом, данная функция имеет множество первообразных, причем можно показать, что любые две из них отличаются друг от друга на постоянное число.

Теорема 1 (о двух первообразных). Если F1(x) и F2(x) — две первообразные функции / (x) на отрезке [я, b], то разность между ними равна постоянному числу.

Из этой теоремы следует, что если найдена какая-либо первообразная F(x) для функции / (x) на некотором промежутке (конечном или бесконечном), то любая другая первообразная этой функции может быть найдена по формуле

Определение 2. Множество первообразных функции f (х) называется неопределенным интегралом от функции f (х) и обозначается символом Jf (х)й? х. Таким образом, по определению имеем:

J f ( х )^х = F ( х ) + C,

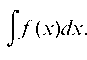
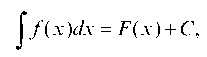
где Д(х) — какая-либо первообразная; C = const; х — независимая переменная интегрирования; f (х) — подинтегральная функция;

f (х)й? х — подинтегральное выражение; J — знак интеграла.

Операция нахождения первообразных функции называется ее интегрированием.

Геометрический смысл неопределенного интеграла. График первообразной Д(х) называют интегральной кривой. В системе координат х0у графики всех первообразных от данной функции представляют семейство кривых, зависящих от величины постоянной С и получаемых одна из другой путем параллельного сдвига вдоль оси 0у. Для примера, рассмотренного выше, имеем:

J 2 х^х = х2 + C.

Семейство первообразных (х + С) геометрически интерпретируется совокупностью парабол.

Если из семейства первообразных нужно найти одну, то задают дополнительные условия, позволяющие определить постоянную С. Обычно с этой целью задают начальные условия: при значении аргумента х = х0 функция имеет значение Д(х0) = у0.

Пример. Требуется найти ту из первообразных функции у = 2 х, которая принимает значение 3 при х0 = 1.

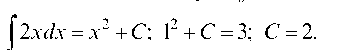
Искомая первообразная: Д(х) = х2 + 2.

Решение. ^2х^х = х2 + C; 12 + С = 3; С = 2.

Теорема 2 (о существовании неопределенного интеграла).

Если функция f (х) непрерывна на отрезке [a, b], то для этой функции существует неопределенный интеграл на этом же отрезке.

1 (f(х )dx) = f (х ).

2. d(ff(x)dx)= f(x)dx,

< Предыдущая		Следующая >